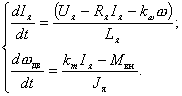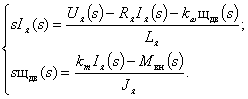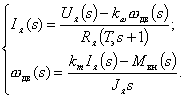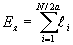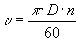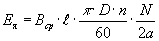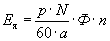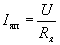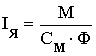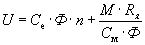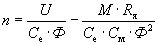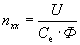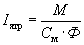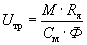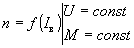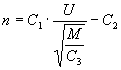Как определить момент на валу двигателя постоянного тока

Вращающий момент электродвигателя

В двигателях постоянного тока вращающий момент определяется выражением М ≡ ФI_я, т.е. он пропорционален потоку и току якоря. В асинхронном двигателе момент создается вращающимся потоком Ф и током ротора I₂. Он может быть выражен

Следовательно, момент пропорционален потоку и активной слагающей тока ротора I₂ cos Ψ₂, так как только активная слагающая тока определяет мощность, а значит и момент.

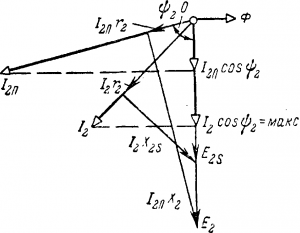
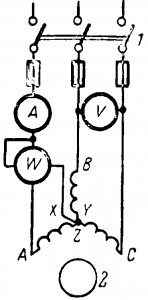
На рис. 10-20 представлена схема включения короткозамкнутого двигателя. Если пустить двигатель, включив рубильник 1, то в первый момент пуска, когда п₂ = 0, a s = 1, наведенная в роторе 2 э. д. с. Е₂ и пусковой ток I_2п максимальны. Однако, пусковой момент М_п не будет максимальным, а в 2—2,5 раза меньше максимального. Векторная диаграмма для цепи ротора (рис. 10-21), построенная подобно изображенной на рис. 9-9, показывает причину этого.

Рис 10-20. Схема включения короткозамкнутого асинхронного двигателя.

Обычно в роторе х₂ во много раз больше r₂ и угол Ψ₂, на который ток I_2п отстает от э. д. с. Е₂ велик. Поэтому активная слагающая тока I_2п cos Ψ₂, а значит и пусковой момент М_п малы. В современных асинхронных двигателях М_п/М_п = 1 — 1,5, хотя I_2п/ I_н≈ 4,5—6,5.

Это же явление по другому объясняется на рис. 10-19 и 10-22.

Рис. 10-21. Векторная диаграмма в цепи ротора.

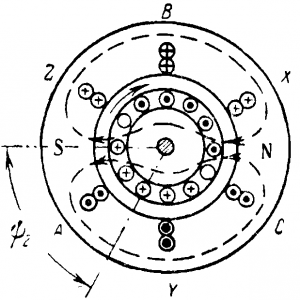
При описании принципа работы двигателя (рис. 10-19) было предположено, что ток I₂ совпадает по фазе с э. д. с. Е₂, т. е. что он активный ( Ψ₂ = 0). На рис. 10-22 представлен момент пуска, когда направление э. д. с. в проводах ротора соответствует обозначенному на рис. 10-19, а ток показан отстающим от э. д. с. на угол Ψ₂. Тогда шесть проводов ротора (три под полюсом N и три под полюсом S) создают усилия, действующие в направлении вращения потока, а два провода вызывают противодействующие усилия. В результате этого вращающий момент будет тем меньше, чем больше сдвиг фаз между током I₂ и э. д. с. E₂.

Рис. 10-22. Ток в роторе двигателя в момент пуска.

По мере увеличения скорости вращения ротора реактивное сопротивление обмотки ротора x₂s = x₂s уменьшается, а вместе с этим уменьшается угол Ψ₂, так как сопротивление r₂ ≈ const. Наступает такое положение (рис 10-21), когда при некотором скольжении s_м ≈ 0,1—0,15 реактивное сопротивление x₂s становится равным активному r₂, угол Ψ — 45° и э. д. с. E_2s уравновешивает два равных падения напряжения I ₂r₂ и I₂x_2s.В это время активная слагающая тока I₂ cos Ψ₂ и вращающий момент М _м становятся максимальными, несмотря на некоторое уменьшение тока I₂.

Обычно М_м/М_м = 1,8—2,5 и называется способностью к перегрузкe.

При дальнейшем разгоне ротора x_2s становится значительно меньшим, чем r₂, им можно пренебречь и считать ток ротора активным (I₂ ≈ I₂ cos Ψ ₂). Так как E_2s = E₂s тоже продолжает уменьшаться, то вместе с током I₂ уменьшается и вращающий момент.

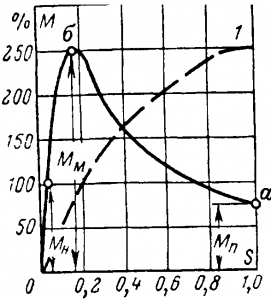
Рис. 10-23. Зависимость вращающего момента двигателя от скольжения.

Нормальная работа двигателя возможна только на участке кривой при скольжениях s от нуля до s_м, так как в этом случае при увеличении тормозного момента и значит s вращающий момент возрастает. На участке от s = s_м до s = 1 работа двигателя неустойчива. Номинальный момент М_н соответствует обычно номинальному скольжению s_н = 1—6%.

Поток Ф пропорционален напряжению U₁, подводимому к трансформатору. Сказанное остается в силе и для асинхронного двигателя. Так как М ≡ ФI₂ cos Ψ ₂, то можно написать, что

Отсюда можно сделать очень важный для асинхронных двигателей вывод

т. е. вращающий момент пропорционален квадрату подведенного к статору напряжения. Таким образом, падение напряжения в сети, например до 0,9 U_1н, вызовет уменьшение момента до 0,9 • 0,9 М_н = 0,81 М_н и нагруженный двига тель может остановиться. Указанным обстоятельством и объясняется, частично, нормирование падения напряжения в распределительных сетях, питающих асинхронные двигатели.

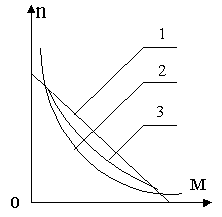
В практике потребителя часто интересует механическая характеристика двигателя

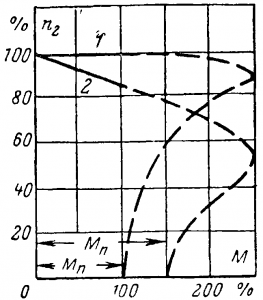
Рис. 10-24. Механическая характеристика двигателя.

Эта характеристика получается простым перестроением рис, 10-23 и показана на рис. 10-24, где рабочая часть обозначена сплошной линией. Кривая 1 для двига телей нормального исполнения показывает, что асинхронный двигатель обладает жесткой характеристикой скорости, подобно двигателю постоянного тока параллельного возбуждения. Асинхронный двигатель с фазным ротором для регулирования скорости вращения, например для крановых и подъемных устройств, имеет более мягкую характеристику (кривая 2).

РАБОЧИЙ ПРОЦЕСС АСИНХРОННОГО ДВИГАТЕЛЯ

рону н. с. со скоростью n₂. Тогда скорость вращения н. с F₂ относительно статора равна:

Таким образом, обе н. с. F₁ и F₂ вращаются с одной скоростью n₁, друг относительно друга неподвижны и создают сообща вращающийся магнитный поток Ф. Следовательно, все приведенное на рис. 9-8 и 9-9 справедливо и для асинхронного двигателя.

Следует отметить, что благодаря воздушному зазору между ротором и статором ток холостого хода (рис. 9-7) двигателя очень велик (20—40)% I_1Н. Поэтому для улучшения cos φ₁ сети двигатель необходимо нагружать полностью.

Статья на тему Вращающий момент электродвигателя

Источник

Определение параметров двигателя постоянного тока независимого возбуждения по каталожным данным

В каталогах [1] на двигатели постоянного тока приводятся следующие технические данные:

– номинальная мощность двигателя, кВт;

– номинальное напряжение обмотки якоря, В;

– номинальный гок обмотки якоря двигателя, А;

– сопротивление обмотки якоря двигателя при 15 °С, Ом;

– сопротивление дополнительных полюсов двигателя при 15 °С, Ом;

– сопротивление компенсационной обмотки двигателя при 15 °С, Ом;

– индуктивность обмотки якоря двигателя, Гн;

– номинальный коэффициент полезного действия, %;

– номинальная частота вращения, об/мин;

– момент инерции якоря, кг•м2.

В тех случаях, когда в каталогах необходимые параметры двигателя не приводятся, их можно определить по следующим формулам:

Номинальный ток двигателя

(3.13)

Номинальная угловая скорость

(3.14)

Сопротивления двигателя приводятся в каталогах при температуре 15 °С. В нагретом состоянии при рабочей температуре сопротивление двигателя

(3.15)

где – температурный коэффициент сопротивления меди (обычно принимается); – рабочая температура обмотки машины; – температура, при которой указываются сопротивления в каталогах. При температуреи, при

(3.16)

Если в каталогах сопротивление двигателя не приведено, то его ориентировочно определяют, принимая, что половина всех потерь в двигателе при номинальной нагрузке связана с потерями в меди якоря [2]. Определенное таким образом сопротивление соответствует нагретому двигателю

(3.17)

Индуктивность цени обмотки якоря двигателя [3]

(3.18)

где р – число пар полюсов двигателя;для быстроходных некомпенсированных машин;для нормальных некомпенсированных машин;для компенсированных машин.

Коэффициент ЭДС и электромагнитного момента при номинальном потоке возбуждения

(3.19)

Номинальный электромагнитный момент двигателя

(3.20)

Номинальный момент двигателя на валу

(3.21)

Пример 3.1. Для двигателя постоянного тока типа ∏-11У4, имеющего следующие технические данные, рассчитать и построить статические электромеханическую и механическую характеристики.

Основные параметры двигателя:

Решение. Так как электромеханическая и механическая характеристики двигателя постоянного тока независимого возбуждения описываются уравнениями прямой, то для их расчета и построения достаточно определить две любые точки. Как правило, координатами этих точек являются: 1) скорость идеального холостого хода ω0 при нулевом токе якоря и электромагнитном моменте; 2) номинальная угловая скоростьпри номинальном токеи номинальном электромагнитном моменте

Определим дополнительные параметры двигателя:

• Номинальная угловая скорость

• Сопротивление якоря двигателя в горячем состоянии

• Коэффициент ЭДС (В ∙ с/рад) и электромагнитного момента (Н • м/A) при номинальном потоке возбуждения

• Угловая скорость идеального холостого хода

• Номинальный электромагнитный момент двигателя

• Пусковой ток или ток короткого замыкания

Рассчитанные статическая естественная электромеханическая и механическая характеристики двигателя приведены на рис. 3.5.

Рис. 3.5. Статические характеристики двигателя постоянного тока независимого возбуждения: а – электромеханические: б – механические

• Допустимый ток двигателя

Вывод. Естественная электромеханическая характеристика двигателя нс обеспечивает ограничение пускового тока на допустимом уровне. Как следствие пуска двигателя прямым включением в сеть – неудовлетворительная коммутация на коллекторе и выход коллектора из строя.

Пример 3.2. Для двигателя постоянного тока типа ∏-11У4 рассчитать и построить динамическую механическую характеристику. Основные параметры двигателя приведены в примере 3.1.

Динамическую механическую характеристику построить при моменте сопротивления на валу двигателя

Решение. В динамике двигатель постоянного тока независимого возбуждения описывается системой уравнения (3.12):

При подстановке в систему уравнений численных значений параметров получим:

(3.22)

Динамическая механическая характеристика пуска двигателя постоянного тока независимого возбуждения прямым включением в сеть, рассчитанная в программной среде MathCAD, приведена на рис. 3.6.

Анализ графика динамической механической характеристики показывает, что максимальное значение пускового момента составляет

Учитывая, что ток якоря двигателя независимого возбуждения пропорционален его моменту, найдем максимальный пусковой динамический ток якоря

Рис. 3.6. Графики статической (1) и динамической (2) характеристик пуска двигателя постоянного тока независимого возбуждения прямым включением в сеть

Максимальный пусковой динамический ток превышает предельно допустимый ток якоря двигателя по условиям коммутации , однако он существенно меньше тока короткого замыкания . Отмеченная особенность уменьшения пусковою динамического тока двигателя независимого возбуждения позволяет электрические машины мощностью до 200 Вт пускать прямым включением в сеть без принятия мер токоограничения.

Источник

Основные теоретические положения

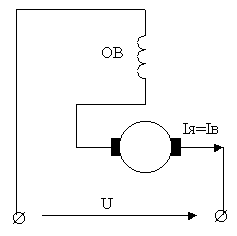
Важное свойство ДПТ с независимым возбуждением от постоянных магнитов состоит в том, что результирующий момент сил от всех проводников якоря, называемый электромагнитным моментом двигателя M, пропорционален току якоря I_я, потребляемому двигателем от источника питания:

,

,

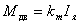
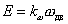
Природа электромагнитных явлений в ДПТ такова, что если используется система единиц СИ, то значения коэффициентов k _ω и k_m численно равны.

Уравнения, описывающие электрические процессы в ДПТ

В электрической якорной цепи двигателя протекает ток I _я под действием напряжения постоянного тока U_a источника питания и противоЭДС двигателя.

Рис. 1

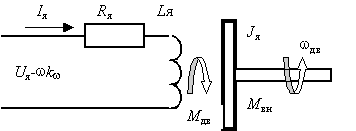
Исходные дифференциальные уравнения ДПТ составляются на основании законов физики. Для электрической цепи используется второй закон Кирхгофа, согласно которому можно записать уравнение

,

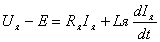
где член R _я I _я характеризует падение напряжения на активном сопротивлении якорной цепи в соответствии с законом Ома, а член L _я ( dI _я/ dt ) отражает наличие ЭДС самоиндукции, возникающей в обмотке при изменении тока якоря. В представленном уравнении не учитывается падение напряжения на щетках, зависящее нелинейно от тока якоря, но имеющее, как правило, относительно небольшое значение по сравнению с напряжением U _я .

Дифференциальное уравнение, характеризующее процессы в механической части двигателя, составляется на основании второго закона Ньютона:

Используя вышеприведенные формулы и приводя дифференциальные уравнения к нормальной форме Коши, получим описание ДПТ в форме:

Для исследования процессов с помощью ЭВМ удобно использовать структурное представление математической модели ДПТ. Для этого преобразуем полученную систему линейных дифференциальных уравнений по Лапласу при нулевых начальных условиях. В результате получим систему алгебраических уравнений:

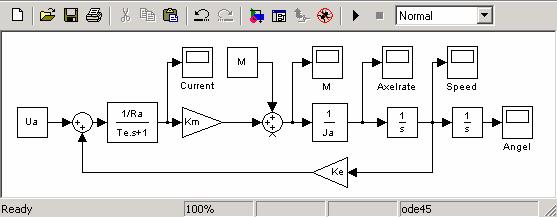
По уравнениям с помощью системы SIMULINK может быть сформирована структурная схема ДПТ для его математического моделирования (рис.1).

Важным параметром ДПТ, определяющим его динамические свойства, является электромеханическая постоянная времени двигателя:

.

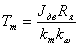
Зависимость между электромагнитным моментом двигателя и частотой вращения ротора в установившемся режиме при постоянных U _я и M _вн называется механической характеристикой двигателя. Уравнение механической характеристики имеет вид:

.

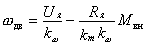
При пуске двигателя, когда скорость равна нулю, развивается пусковой момент

Частота вращения вала двигателя при отсутствии сопротивления называется частотой вращения холостого хода

Источник

Как определить момент на валу двигателя постоянного тока

Микроэлектродвигатели постоянного тока.

В современных радиоэлектронных, оптических, механических и т. п. портативных аппаратах, снабжённых автономными источниками электрической энергии, а также во многих стационарных устройствах широко используются микроэлектродвигатели постоянного тока. Такие преимущества этих двигателей, как линейность механических характеристик, хорошие регулировочные свойства, большой пусковой момент, высокое быстродействие и хорошие весогабаритные показатели позволяют использовать эти двигатели в качестве исполнительных двигателей устройств автоматики.

Недостатком этих двигателей является наличие щёточно – кол-лекторного устройства, практически исключающего возможность использования ДПТ в условиях агрессивных и взрывоопасных сред и удорожающего обслуживания устройств ДТП.

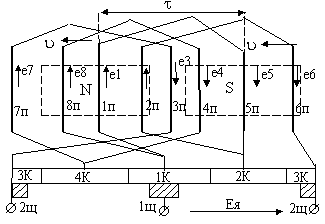
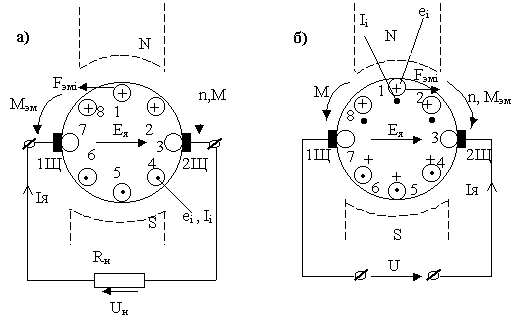
Конструктивно ДПТ состоит из статора (неподвижной части) и ротора или якоря (вращающейся части), помещённого внутри статора. Упрощённо конструкцию машины можно пояснить с помощью рис.6.1.

Статор состоит из стальной станины 1, на внутренней поверхности которой расположены главные полюса, состоящие из сердечников 2 и катушек возбуждения 3. В нижней части сердечника полюса имеется полюсный наконечник 4, который обеспечивает нужное распределение магнитной индукции в воздушном зазоре машины. К станине с торцевых сторон прикреплены подшипниковые щиты ( на рис. 6.1 не показаны ), к одному из которых прикреплены щёткодержатели с металлографитовыми щётками 9.

Ротор ( якорь ) ДПТ состоит из сердечника 5, обмотки якоря 6, коллектора 7 и вала 8.

Сердечник 5 представляет собой цилиндр, набранный из штампованных листов электротехнической стали с отверстием под вал двигателя и с пазами, в которых укладываются проводники обмотки якоря.

Коллектор 7 – цилиндр, набранный из медных пластин трапеци-евидного сечения, изолированных электрически друг от друга и от вала двигателя.

Обмотка якоря машины представляет собой замкнутую систему проводников, уложенных и укреплённых в пазах сердечника 5. Она состоит из секций (катушек), выводы которых соединены с двумя коллекторными пластинами. У микромашин обычного исполнения с одной парой полюсов на статоре обмотка якоря представляет собой простую петлевую обмотку (схема рис.6.2), при построении которой выводы секций обмоток присоединяются к двум соседним коллекторным пластинам, а число секций обмотки и число коллекторных пластин коллектора одинаково.

Магнитная цепь ДПТ.

Принцип действия ДПТ основан на взаимодействии тока провод-ников обмотки якоря с магнитным полем возбуждения, в результате чего на каждый проводник обмотки якоря действует электромеханическая сила, а совокупность сил, действующих на все активные проводники обмотки, образует электромагнитный момент машины.

Магнитное поле возбуждения формируется магнитной цепью машины. Магнитная цепь машины – разветвленная, симметричная, неоднородная. Намагничивающая сила создается током, протекающим через обмотки главных полюсов машины. Магнитный поток проходит 5 участков: сердечники главных полюсов, воздушный зазор, зубцовый слой якоря, тело якоря и станина (рис. 6.1). Поскольку намагничивающая сила и, следовательно, поток постоянны, то нет необходимости делать станину шихтованной (отсутствуют потери на вихревые токи). Работающие в условиях пульсирующего магнитного потока сердечники главных полюсов, полюсные наконечники и сердечник ротора выполняются шихтованными с целью снижения потерь на вихревые токи.

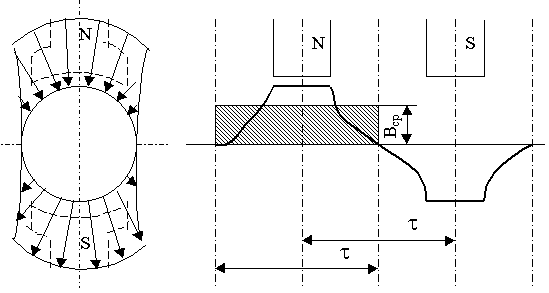
В ДПТ используется индукция магнитного поля, нормальная к поверхности якоря. Под полюсами эта индукция – максимальна, посередине между полюсами – равна 0.

Линия dd, проходящая через середины полюсов и центр якоря называется продольной магнитной осью машины, а линия, проходящая посередине между смежными полюсами называется поперечной магнитной осью или геометрической нейтралью.

,

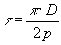
где D – диаметр ротора.

График распределения нормальной к поверхности якоря индукции в воздушном зазоре машины на развернутом полюсном делении приведен на рис. 6.3 и имеет трапециедальный вид.

Электродвижущая сила и электромагнитный момент ДПТ.

При вращении ротора ДПТ в каждом активном проводнике обмотки якоря, пересекающем нормальные к его поверхности силовые линии магнитного поля полюсов наводятся ЭДС с направлением определяемым по правилу правой руки и величиной, определяемой выражением

,

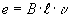
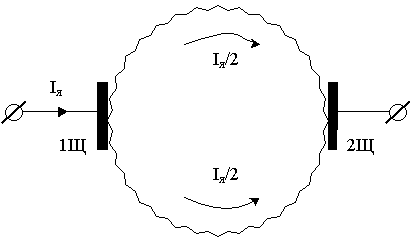
Таким образом для двухполюсной машины обмотка якоря по отношению к щёткам имеет две параллельных ветви, ЭДС в проводниках которых направлены согласно. Несмотря на то, что при вращении ротора всё новые и новые проводники будут образовывать параллельные ветви, направление ЭДС в проводниках, а также направление суммарной ЭДС параллельной ветви или ЭДС якоря Ея остаётся неизменной при неизменном направлении вращения ротора.

Поскольку число активных проводников параллельной ветви составляет десятки и даже сотни, то несмотря на пульсирующий характер ЭДС каждого из проводников суммарная ЭДС

остается практически постоянной при постоянной скорости вращения ротора. В таком случае можно воспользоваться значением средней индукции в воздушном зазоре машины В ср и найти ЭДС ее как

,

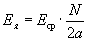
где 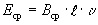— среднее значение ЭДС в каждом проводнике обмотки,

N/2a- число проводников параллельной ветви.

Зная, что линейная скорость равна

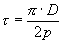
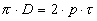
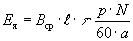
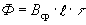
Т.к. полюсное деление , то .

.

.

Тогда ЭДС Ея можно найти в виде

,

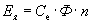
где 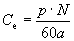— конструктивная постоянная машины.

Таким образом, ЭДС якоря машины пропорциональна величине магнитного потока полюсов и частоте вращения ротора. При постоянном магнитном потоке Ф ЭДС якоря машины пропорциональна частоте вращения ротора, т.е.

,

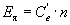
что дает возможность использовать такую машину в качестве датчика частоты вращения или тахогенератора.

,

На каждый проводник с током, помещенный в магнитное поле машины действует электромагнитная сила

,

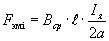
а совокупность сил действующих на все N проводников ротора приводит к возникновению результирующего электромагнитного момента машины

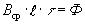
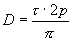
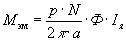
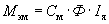
Т.к. , а , то после подстановки получим

.

,

где — моментная конструктивная постоянная машины.

Таким образом, электромагнитный момент, развиваемый ДПТ пропорционален магнитному потоку Ф и току якоря машины.

Режимы работы и основные уравнения ДПТ.

Любая машина постоянного тока обладает свойством обратимости, т.е. она может работать как в генераторном, так и в двигательном режиме при изменении знака момента нагрузки на ее валу или при изменении напряжения на якоре.

Генераторный режим работы машины – такой режим, при котором ток якоря и ЭДС Ея совпадают по направлению, а электромагнитный момент, развиваемый машиной противоположен по направлению враще-нию ротора. Такой режим имеет место, если ротор ДПТ разогнать от внешнего момента М до скорости n и замкнуть цепь якоря на сопротивление нагрузки Rн (рис. 6.5,а).

При работе машины в генераторном режиме ЭДС якоря уравновешивается падением напряжения на нагрузке и падением напряжения от тока якоря на сопротивлении якоря, т. е.

,

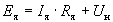
Уравнение баланса мощностей при работе машины в генераторном режиме имеет вид

,

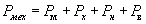
где Рмех – механическая мощность, потребляемая машиной от источника механической мощности, Рм – потери мощности в обмотке якоря, Рх – потери холостого хода, состоящие из потерь на трение в подшипниках и потерь на перемагничивание материала ротора, Рн – электрическая мощность в нагрузке, Рв – потери в меди обмотки возбуждения.

Двигательный режим работы – такой режим, при котором элекромагнитный момент машины Мэм совпадает по направлению со скоростью, а ЭДС якоря Ея направлена встречно току якоря.

, где

.

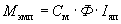
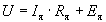
При этом 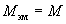и якорь будет вращаться с постоянной скоростью.

Уравнение баланса мощности для двигательного режима работы имеет вид

,

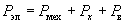
Основные характеристики ДПТ.

В зависимости от способа возбуждения различают ДПТ с независимым (или параллельным) возбуждением, с последовательным возбуждением и со смешанным возбуждением.

Характеристики ДПТ с независимым возбуждением.

Характерной особенностью таких двигателей является независимость тока возбуждения (или потока возбуждения) от тока якоря машины. Разновидностью независимого возбуждения является возбуждение от постоянных магнитов.

Механические характеристики ДПТ с независимым возбуждением:

и или

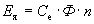
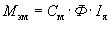
основное уравнение ДПТ в двигательном режиме работы

можно привести к виду

,

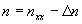
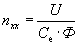
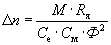
где — скорость идеального холостого хода машины,

-изменение скорости, обусловленное моментом нагрузки двигателя.

Как следует из уравнения механической характеристики, скорость двигателя при постоянном моменте нагрузки можно регулировать тремя способами:

1.Изменением напряжения на якоре двигателя,

2.Изменением сопротивления в цепи якоря двигателя,

3.Изменением потока возбуждения машины.

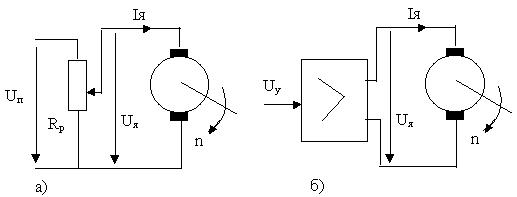
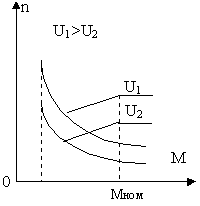
При регулировании скорости первым из названных способов, напряжение на якоре изменяется либо с помощью реостата (рис.6.7,а), либо с помощью усилительно –преобразовательного устройства (рис.6.7,б), при этом поток возбуждения остаётся постоянным.

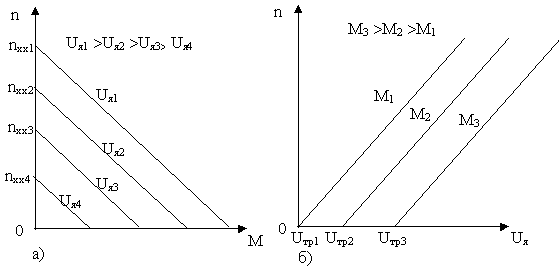
Семейство механических характеристик, соответствующих данному способу регулирования, приведено на рис.6.8.

С изменением напряжения U пропорционально изменяется и скорость холостого хода

при этом угол наклона (или жестокость) механических характеристик остаётся неизменной.

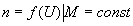
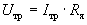
Регулировочная характеристика линейна при напряжении на якоре U > U тр имеет зону нечувствительности при напряжении на якоре U тр, где –напряжение трогания двигателя. Дело в том, что двигатель не будет вращаться до тех пор, пока , а для создания такого момента необходимо иметь ток якоря

Для создания такого тока при скорости вращения n=0 необходимо иметь на якоре напряжение

Несмотря на то, что рассмотренный способ регулирования требует довольно сложного оборудования, его широко применяют в современных электроприводах, т.к. он обеспечивает плавное и экономичное регулирование скорости в широких пределах при сохранении высокой жесткости механических характеристик. Лучшие современные системы при данном способе обеспечивают диапазон до 1:100000.

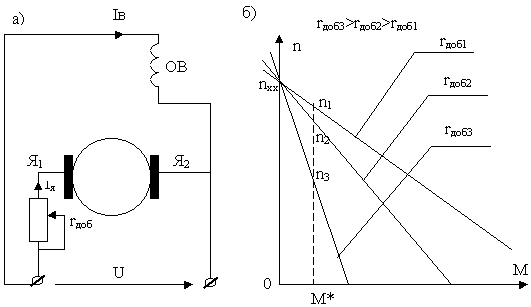
Регулирование скорости по второму из указанных способов осуществляется изменением величины добавочного сопротивления , включённого последовательно в цепь якоря машины (рис.6.9,а).

Семейство механических характеристик при данном способе регулирования приведено на рис. 6.9,б.

С увеличением увеличивается угол наклона механической характеристики к оси абсцисс, при этом заданному моменту нагрузки соответствуют различные скорости вращения ротора. Скорость холостого хода в данном случае не изменяется. Достоинство такого способа регулирования скорости – простота схемной и аппаратурной реализации, недостатки- большие потери энергии в добавочном сопротивлении, узкий диапазон регулирования скорости при малых моментах нагрузки и малая жесткость механических характеристик при больших сопротивлениях . Регулировочная характеристика нелинейна.

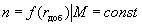
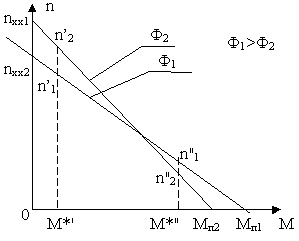
Регулирование скорости вращения третьим способом можно осуществить по схеме, приведённой на рис. 6.10.

В цепь обмотки возбуждения включается добавочный реостат для регулирования тока возбуждения двигателя, напряжение на якоре остаётся при этом неизменным. В силу того, что 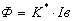, то при изменении Iв изменяется как скорость холостого хода, так и значение пускового момента М п.

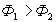
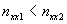
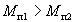
Следовательно при , и , механические характеристики, соответствующие двум значениям потока возбуждения можно изобразить в виде рис. 6-11.

Ввиду того, что механические характеристики, соответствующие различным значениям потока возбуждения пересекаются между собой, то при малых моментах нагрузки скорость может возрастать с уменьшением потока, а при больших –падать. Регулировочная характеристика

для случая идеального холостого хода представлена кривой 1 на рис. 6.12.

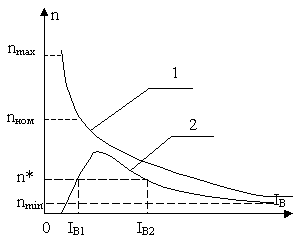
В ДПТ с последовательным возбуждением поток возбуждения создаётся током якоря машины, для чего обмотка возбуждения и якорь двигателя включаются последовательно относительно источника питания, как показано на схеме рис. 6.13.

Обычно при токах 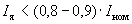магнитная цепь машины не насыщена и поток возбуждения пропорционален току возбуждения

.

При больших токах якоря 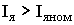магнитная цепь машины насыщена, и поток возбуждения можно считать постоянным.

Подставив в уравнение

,

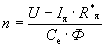
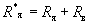
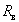
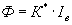
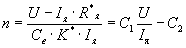
где , а — сопротивление обмотки возбуждения, значение , получим

.

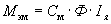
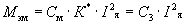
Зная, что , получим

,

где – постоянные.

Поскольку в установившемся режиме 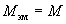, то

и уравнение механической характеристики ДПТ с последовательным возбуждением в диапазоне нагрузок 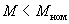принимает вид

которому соответствует гиперболическая кривая, приведённая на рис. 6.14.

Способность двигателей последовательного возбуждения развивать большой электромагнитный момент, пропорциональный квадрату тока якоря, обеспечивает этим двигателям хорошие пусковые свойства, т. е. большой пусковой момент при сравнительно малом токе якоря. Поэтому такие двигатели применяют в грузоподъёмных и тяговых приводах. Следует обратить внимание на недопустимость работы электродвигателей с последовательным возбуждением в режиме холостого хода или с нагрузкой, менее 25% от номинальной – это приводит к разносу двигателя.

Регулирование скорости вращения этих двигателей возможно теми же способами, что и для двигателей с независимым возбуждением.

В этих двигателях магнитный поток Ф создаётся в результате совместного действия двух обмоток возбуждения – параллельной и последовательной (рис.6.15), поэтому механическая характеристика (кривая 3 на рис.6.1,6) располагается между характеристиками двигателя с независимым возбуждением (кривая 1) и двигателя с последовательным возбуждением (кривая 2).

Источник