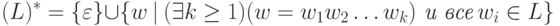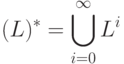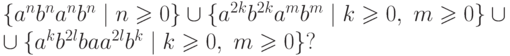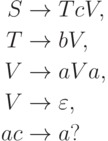Пример языка не являющегося регулярным
Лемма о разрастании для регулярных языков
В теории формальных языков большое значение имеют утверждения, в которых формулируется необходимое условие принадлежности языка к тому или иному классу языков. Эти утверждения известны в литературе под названием лемм о разрастании (или лемм о «накачке»). С помощью этих лемм удается доказать, что тот или иной язык не является языком данного класса, например, не является регулярным, контекстно-свободным и т.п. Доказывать подобного рода «отрицательные» утверждения гораздо труднее, чем «положительные» (что язык есть язык данного класса ), ибо в последнем случае требуется придумать любую грамматику соответствующего класса, порождающую данный язык, а в первом нужно каким-то образом доказать, что не существует грамматики этого класса, порождающей язык. Применение лемм о разрастании состоит в следующем: доказав, что предлагаемый язык не удовлетворяет условию леммы о разрастании, мы можем быть уверены в том, что он заведомо не принадлежит соответствующему классу языков, и нам нечего и пытаться искать для него грамматику того же класса.
Мы рассмотрим подобного рода утверждения для классов регулярных, контекстно-свободных и линейных языков.
Начнем с леммы о разрастании для регулярных языков. Эта лемма (см. теорему 7.10) утверждает, что любой регулярный язык допускает представление всех своих достаточно длинных цепочек в виде соединения трех цепочек, причем средняя цепочка из этих трех не пуста, ограничена по длине, и ее «накачка» — повторение любое число раз — или выбрасывание не выводит за пределы языка (т.е. дает цепочки, принадлежащие данному регулярному языку).
2) контур, проходящий через ;
Примеры доказательств нерегулярности языка
Ясно, что накачка в этом случае выведет за пределы языка, так как при повторении цепочки число символов будет неограниченно расти, а число символов будет оставаться прежним.
Накачка невозможна по той же причине, что и в предыдущем случае.
Полезно иметь в виду следствие из леммы о разрастании.
Следствие 7.4. Если — бесконечный регулярный язык, то в нем найдется последовательность слов, длины которых образуют возрастающую арифметическую прогрессию.
В качестве такой последовательности можно взять последовательность слов из формулировки леммы о разрастании. Их длины образуют арифметическую прогрессию со знаменателем (длина «накачиваемой» средней подцепочки).
Отсюда легко получается вывод о том, что не являются регулярными следующие языки:
Можно доказать, что любой конечный язык регулярен и, более того, допускается конечным автоматом без контуров. Значит, последовательность цепочек, указанная в формулировке леммы, в таком случае не существует, но утверждение леммы остается истинным. Нужно всегда помнить простое логическое правило: утверждение вида «если А, то Б» равносильно утверждению вида «не А или Б».
В заключение обсудим еще одну схему доказательства нерегулярности языка с использованием как леммы о разрастании, так и алгебраических свойств класса регулярных языков, которые были установлены ранее.
Пример 7.13. Докажем нерегулярность языка правильных скобочных структур, порождаемых КС-грамматикой
Замечание 7.12. С использованием «техники пересечения» можно доказать нерегулярность языка из примера 7.12 следующим образом. Так как язык
нерегулярный, то и язык тоже не является регулярным.
Итак, можно вывести такой «рецепт»: если возникают существенные затруднения в доказательстве нерегулярности какого-либо языка с помощью только леммы о разрастании, то можно попытаться пересечь этот язык с некоторым регулярным языком так, чтобы нерегулярность пересечения легко доказывалась с использованием леммы о разрастании.
Регулярные языки и конечные автоматы
Регулярные выражения и языки
Тогда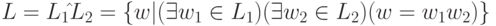 
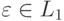
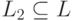
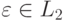
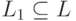
, т.е. конкатенация языков состоит из конкатенаций всех слов первого языка со всеми словами второго языка. В частности, если 
, то 
, а если 
, то 
.
Введем обозначения для «степеней» языка L :
Итерацию (L) * языка L образуют все слова которые можно разбить на несколько подряд идущих слов из L :
Ее можно представить с помощью степеней:
Отметим также, что если рассматривать алфавит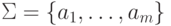 
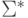
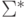
как конечный язык, состоящий из однобуквенных слов, то введенное ранее обозначение 
для множества всех слов, включая и пустое, в алфавите 
соответствует определению итерации 
этого языка.
В следующей таблице приведено формальное индуктивное определение регулярных выражений над алфавитом и представляемых ими языков.
Нетрудно проверить, например, такие свойства регулярных операций:
Рассмотрим несколько примеров регулярных выражений и представляемых ими языков.
Пример 5.2. Регулярное выражение (0 +1) * представляет множество всех слов в алфавите <0, 1>.
Пример 5.3. Регулярное выражение 11(0 +1) * 001 представляет язык, состоящий из всех слов в алфавите <0, 1>, которые начинаются на ’11’, а заканчиваются на ‘001’.
Пример 5.4. Регулярное выражение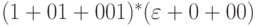 
представляет язык, состоящий из всех слов в алфавите <0, 1>, которые не содержат подслово ‘000’ ( см. задачу 5.3).
Основные свойства контекстно-свободных языков
В «лекции 2» были доказаны лемма о разрастании и свойства замкнутости класса автоматных языков. Некоторые из этих теорем имеют аналоги для класса контекстно-свободных языков ( разделы 9.1 и 9.4), но этот класс не замкнут относительно дополнения и пересечения (раздел 9.5).
Лемма о разрастании для контекстно-свободных языков формализует явление «периодичности» в этих языках. Для полноты картины в разделах 9.2* и 9.3 приведены некоторые аналогичные теоремы для класса линейных языков, хотя ни в теории, ни в практических приложениях класс линейных языков значительной роли не играет.
В разделе 9.6 доказывается, что пересечение контекстно-свободного языка с автоматным языком является контекстно-свободным. В сочетании с леммой о разрастании этот факт дает удобное средство, позволяющее во многих задачах доказать, что заданный язык не является контекстно-свободным. Еще одно необходимое условие контекстной свободности сформулировано в разделе 9.7*.
9.1. Лемма о разрастании для контекстно-свободных языков
Теорема 9.1.3. Каждый контекстно-свободный язык над однобуквенным алфавитом является автоматным.
Упражнение 9.1.4. Является ли контекстно-свободным язык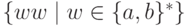 
?
Упражнение 9.1.5. Является ли контекстно-свободным язык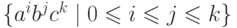 
?
Упражнение 9.1.6. Является ли контекстно-свободным язык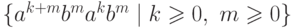 
?
Упражнение 9.1.7. Является ли контекстно-свободным язык ?
Упражнение 9.1.8. Является ли контекстно-свободным язык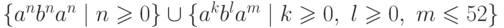 
?
Упражнение 9.1.9. Является ли контекстно-свободным язык 
?
Упражнение 9.1.10. Является ли контекстно-свободным язык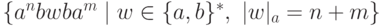 
?
Упражнение 9.1.11. Является ли контекстно-свободным язык 
?
Упражнение 9.1.12. Является ли контекстно-свободным язык 
?
Упражнение 9.1.15. Является ли контекстно-свободным язык
Упражнение 9.1.16. Какому классу принадлежит язык, порождаемый грамматикой
Упражнение 9.1.17. Существуют ли такие контекстно-свободные языки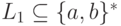 
и 
, что язык 
не является контекстно-свободным?
Регулярные языки и конечные автоматы
Регулярные выражения и языки
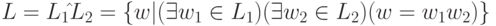
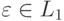
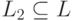
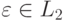
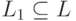
Тогда , т.е. конкатенация языков состоит из конкатенаций всех слов первого языка со всеми словами второго языка. В частности, если , то , а если , то .
Введем обозначения для «степеней» языка L :
Итерацию (L) * языка L образуют все слова которые можно разбить на несколько подряд идущих слов из L :
Ее можно представить с помощью степеней:
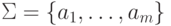
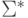
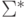
Отметим также, что если рассматривать алфавит как конечный язык, состоящий из однобуквенных слов, то введенное ранее обозначение для множества всех слов, включая и пустое, в алфавите соответствует определению итерации этого языка.
В следующей таблице приведено формальное индуктивное определение регулярных выражений над алфавитом и представляемых ими языков.
Нетрудно проверить, например, такие свойства регулярных операций:
Рассмотрим несколько примеров регулярных выражений и представляемых ими языков.
Пример 5.2. Регулярное выражение (0 +1) * представляет множество всех слов в алфавите <0, 1>.
Пример 5.3. Регулярное выражение 11(0 +1) * 001 представляет язык, состоящий из всех слов в алфавите <0, 1>, которые начинаются на ’11’, а заканчиваются на ‘001’.
Пример 5.4. Регулярное выражение 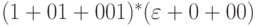представляет язык, состоящий из всех слов в алфавите <0, 1>, которые не содержат подслово ‘000’ ( см. задачу 5.3).
Лемма о накачке для регулярных языков
В теории формальных языков, лемма о накачке для регулярных языков описывает существенное свойство всех регулярных языков. Неформально она утверждает, что все достаточно длинные слова регулярного языка можно накачать, то есть повторить внутреннюю часть слова сколько угодно раз, производя новое слово, также принадлежащее языку.
Лемма о накачке впервые сформулировал Иешуа Бар-Хиллель, Перлес и Шамир в 1961 году. [1] Она полезна для опровержения регулярности заданного языка. Она является одной из нескольких лемм о накачке, у каждой из которых похожее предназначение.
Содержание
Формальное утверждение
Пусть L регулярный язык. Тогда существует целое p ≥ 1 зависящее только от L, такое что любая строка w из L длины по меньшей мере p (p называется «длиной накачки») может быть записано как w = xyz, так что:
y — это подстрока, которую можно накачать (удалить или повторить произвольное число раз, так что результат останется в L). (1) означает, что цикл y должен быть накачан хотя бы длиной 1, (2) означает, что цикл должен быть в пределах первых p символов. На x и z ограничений не накладывается.
Неформальное утверждение и пояснение
Лемма о накачке описывает существенное свойство регулярных языков. Она утверждает, что слово w языка L длины по меньшей мере m, (где m константа, называемая длиной накачки, зависит лишь от L) можно разделить на три подстроки, 
, так что среднюю часть, y (непустую), можно повторить произвольное число раз (включая ноль, то есть удалить) и получить строку из L. Этот процесс повторения называется «накачкой». Более того, лемма о накачке гарантирует, что длина xy не превысит m, ограничивая способы разделения строки w. Заметим, что конечные языки удовлетворяют требованиям леммы о накачке тривиально определяя m длиной максимальной строки из языка плюс один.
Использование леммы
Лемма о накачке часто используется для доказательство того, что некоторый язык не является регулярным: доказательство от противного (предположив регулярность языка) может состоять из нахождения слова (нужной длины) языка, для которого свойство из формулировки леммы не выполняется.
Доказательство нерегулярности языка сбалансированных скобок проводится с той же идеей. Если дано p, существует строка сбалансированных скобочек, начинающихся с более чем p левых скобок, так что y будет содержать только левые скобки. Повторяя y, можно сконструировать строку, в которой не содержится равное количество левых и правых скобок, которая не может быть сбалансированной.
Доказательство леммы о накачке
Для каждого регулярного языка существует конечный автомат (КА), принимающий этот язык. Если язык конечен, то результат можно получить немедленно, просто задав длину накачки p более длины самого длинного слова языка: в этом случае нет ни одной строки в языке длиннее p, и утверждение леммы выполняется безусловно.
Если регулярный язык бесконечен, то существует минимальный КА, его принимающий. Число состояний этого КА и принимается за длину накачки p. Если длина строки превышает p, то хотя бы одно состояние при обработке строки повторяется (назовём его S). Переходы из состояния S и обратно соответствуют некоторой строке. Эту строку обозначим y по условиям леммы, и поскольку автомат примет строку как без части y, так и с повторяющейся частью y, условия леммы выполнены.
Проще понять доказательство, обратившись к примеру. На следующей диаграмме показан КА.
Этот КА принимает строку abcbcd. Поскольку длина её превышает число состояний, существуют повторяющиеся состояния. В этом примере повторяются состояния q1 и q2. Поскольку подстрока bcbc строки abcbcd проводит автомат по переходам из состояния q1 обратно в q1, эту строку можно повторять сколько угодно раз, и КА всё равно будет её принимать, например строки abcbcbcbcd и ad. В терминах леммы о накачке, строка abcbcd разбивается на часть x=a, часть y=bc и часть z=bcd. (Заметим, что можно разбить её различными способами, например x=a, y=bcbc, z=d, и все условия будут выполнены, кроме |xy| ≤ p).
Обобщённая лемма о накачке для регулярных языков
Если язык L регулярен, то существует число p > 0 (длина накачки), такое что для любой строки uwv из L с |w| ≥ p справедливо представление
uxy i zv принадлежит L для любого целого i ≥ 0.
Эту версию можно использовать для доказательства нерегулярность ещё большего числа языков, так как она накладывает более строгие ограничения.
Недостаточность леммы
Заметим, что ни исходная, ни обобщённая леммы о накачке не дают достаточного условия регулярности языка. Так, существуют нерегулярные языки, для которых лемма выполнена. Если лемма не выполняется для некоторого языка L, то L нерегулярен. Если лемма выполняется для L, то L может быть регулярным.
Для практического характеризующего регулярность языка, можно использовать теорему Майхилла-Нерода. Типичный метод доказательства регулярности языка заключается в построении либо конечного автомата, либо регулярного выражения для языка.