Примеры алгоритмов на естественном языке
Запись алгоритма на естественном языке
Свойства алгоритма
Алгоритм обладает следующими основными свойствами: дискретностью, определенностью, результативностью, массовостью.
Дискретность. Процесс преобразования исходных данных в результат осуществляется дискретно, так что значения величин в каждый следующий момент времени получаются по определенным правилам из значений величин, имевшихся в предшествующий момент времени.
Определенность (или детерминированность). Каждое правило алгоритма должно быть четким и однозначным, так что значения величин, получаемые в какой-либо (не начальный) момент времени, однозначно определяются значениями величин, полученными в предыдущие моменты времени.
Результативность (или конечность). Алгоритм должен приводить к решению задачи за конечное число шагов.
Массовость. Алгоритм решения задачи разрабатывается в общем виде так, чтобы его можно было применить для класса задач, различающихся лишь исходными данными. При этом исходные данные могут выбираться из некоторой области, называемой областью применимости алгоритма. Например, приведенный выше алгоритм решения квадратного уравнения применим для различных наборов коэффициентов a, b, c.
Чтобы разработать алгоритм, нужно хорошо представлять себе ход решения задачи и затем формализовать, т.е. записать в виде последовательности четких правил. Понятия алгоритма и программы не очень четко разграничены. Обычно программа – это окончательный вариант алгоритма решения задачи, ориентированный для конкретной вычислительной машины.
При разработке алгоритма его можно фиксировать несколькими способами:
1. запись на естественном языке (см. предыдущие примеры);
2. изображение в виде схемы;
3. запись на языке программирования.
Хотя естественный язык не требует детальных разъяснений и полной формализации, ниже сформулированы некоторые правила, которые облегчат в дальнейшем переход к языкам программирования.
Типичные действия (команды) алгоритма записываются следующим образом.
1. Команда обработки (вычисления):
где v и x – переменные. Эта команда служит для вычисления выражения, стоящего в правой части, либо для выполнения какого-либо действия. Вообще, любые действия, вычисления и изменение значений переменных можно выполнить только на этом этапе.
2. Проверка условия:
Если условие идти к N
Если условие выполняется, то осуществляется переход к команде с номером N. Если условие не выполняется, то переходят к следующей по порядку команде.
Урок 15
§ 2.2. Способы записи алгоритмов
Ключевые слова:
• словесное описание
• построчная запись
• блок-схема
• школьный алгоритмический язык
Существуют различные способы записи алгоритмов. Основными среди них являются:
• словесные;
• графические;
• на алгоритмических языках.
Теоретические исследования нашего соотечественника Андрея Андреевича Маркова (младшего) (1903-1979), выполненные в середине прошлого века, показали, что в общем случае алгоритмы должны содержать предписания двух видов:
1) предписания, направленные на непосредственное преобразование информации (функциональные операторы);
2) предписания, определяющие дальнейшее направление действий (логические операторы).
Именно эти операторы положены в основу большинства способов записи алгоритмов.
2.2.1. Словесные способы записи алгоритма
Словесное описание. Самой простой является запись алгоритма в виде набора высказываний на обычном разговорном языке. Словесное описание имеет минимум ограничений и является наименее формализованным. Однако все разговорные языки обладают неоднозначностью, поэтому могут возникнуть различные толкования текста алгоритма, заданного таким образом. Алгоритм в словесной форме может оказаться очень объёмным и трудным для восприятия.
Пример 1. Словесное описание алгоритма нахождения наибольшего общего делителя (НОД) пары натуральных чисел (алгоритм Евклида).
Чтобы найти НОД двух чисел, составьте таблицу из двух столбцов и назовите столбцы X и У. Запишите первое из заданных чисел в столбец X, а второе — в столбец У. Если данные числа не равны, замените большее из них на результат вычитания из большего числа меньшего. Повторяйте такие замены до тех пор, пока числа не окажутся равными, после чего число из столбца X считайте искомым результатом.
Построчная запись. Это запись на естественном языке, но с соблюдением некоторых дополнительных правил:
• каждое предписание записывается с новой строки;
• предписания (шаги) алгоритма нумеруются;
• исполнение алгоритма происходит в порядке возрастания номеров шагов, начиная с первого (если не встречается никаких специальных указаний).
Кроме слов естественного языка предписания могут содержать математические выражения и формулы.
Пример 2. Построчная запись алгоритма Евклида.
1. Обозначить первое из заданных чисел X, второе обозначить Y.
2. Если X = Y, то перейти к п. 8.
3. Если X > Y, то перейти к п. 4, иначе перейти к п. 6.
8. Считать X искомым результатом.
Построчная запись алгоритма позволяет избежать ряда неопределённостей; её восприятие не требует дополнительных знаний.
Вместе с тем использование построчной записи требует от человека большого внимания.
2.2.2. Блок-схемы
Наилучшей наглядностью обладают графические способы записи алгоритмов; самый распространённый среди них — блок-схема.
Блок-схема представляет собой графический документ, дающий представление о порядке работы алгоритма. Здесь предписания изображаются с помощью различных геометрических фигур, а последовательность выполнения шагов указывается с помощью линий, соединяющих эти фигуры. Направления линий связи слева направо и сверху вниз считаются стандартными, соответствующие им линии связи можно изображать без стрелок. Линии связи справа налево и снизу вверх изображаются со стрелками.
Рассмотрим некоторые условные обозначения, применяемые в блок-схемах.
Выполнение алгоритма всегда начинается с блока начала и оканчивается при переходе на блок конца (рис. 2.2, а). Из начального блока выходит одна линия связи; в конечный блок входит одна линия связи.
Внутри блока данных (рис. 2.2, б) перечисляются величины, значения которых должны быть введены (исходные данные) или выведены (результаты) в данном месте схемы. В блок данных входит одна линия связи, и из блока исходит одна линия связи.
В блоке обработки данных (рис. 2.2, в) содержится описание тех действий, которые должны быть выполнены при переходе на этот блок (выполнение определённой операции или группы операций, приводящее к изменению значения, формы или размещения информации). В блок обработки данных входит одна линия связи, и из блока исходит одна линия связи.
Проверка условия изображается с помощью блока принятия решения, внутри которого записывается это условие (рис. 2.2, г). В блок принятия решения входит одна линия, а выходят две линии, около которых записываются результаты проверки условия.
Комментарии (рис. 2.2, д) используются для добавления пояснительных записей, делающих блок-схему более понятной.
Рис. 2.2. Обозначения на блок-схемах
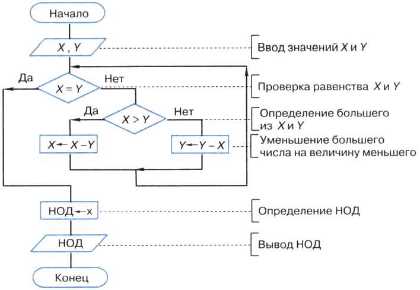
Пример 3. Запись алгоритма Евклида с помощью блок-схемы (рис. 2.3).
Рис. 2.3. Запись алгоритма Евклида с помощью блок-схемы
Создание детальной блок-схемы сложного алгоритма — трудоёмкая задача. Кроме того, блок-схема, не умещающаяся на одном стандартном листе, теряет своё основное преимущество — наглядность. При разработке сложных алгоритмов блок-схемы удобно использовать в качестве средства для наглядного представления решения задачи в общем виде.
2.2.3. Алгоритмические языки
Алгоритмические языки — формальные языки, предназначенные для записи алгоритмов. Каждый из них характеризуется:
• алфавитом — набором используемых символов;
• синтаксисом — системой правил, по которым из символов алфавита образуются правильные конструкции языка;
• семантикой — системой правил, строго определяющей смысл и способ употребления конструкций языка.
Класс алгоритмических языков очень широк. При изучении курса информатики в школах используются различные версии школьного (учебного) алгоритмического языка.
Школьный алгоритмический язык. Для записи алгоритмов на школьном алгоритмическом языке используется некоторое ограниченное множество слов, смысл и способ употребления которых заданы раз и навсегда. Это так называемые служебные слова: алг (алгоритм), дано, надо, нач (начало), кон (конец), арг (аргумент), рез (результат) и др. При записи алгоритмов в книгах служебные слова выделяются жирным шрифтом, в тетради и на доске — подчёркиванием.
В общем виде программу на школьном алгоритмическом языке можно представить так:
Пример 4. Алгоритм, позволяющий из полного сосуда ёмкостью 12 л отлить половину, пользуясь двумя пустыми сосудами ёмкостью 8 и 5 л.
алг переливания
наполнить сосуд ёмкостью 8 л из сосуда ёмкостью 12 л
наполнить сосуд ёмкостью 5 л из сосуда ёмкостью 8 л
вылить всё из сосуда ёмкостью 5 л в сосуд ёмкостью 12 л
вылить всё из сосуда ёмкостью 8 л в сосуд ёмкостью 5 л
наполнить сосуд ёмкостью 8 л из сосуда ёмкостью 12 л
долить из сосуда ёмкостью 8 л в сосуд ёмкостью 5 л
вылить всё из сосуда ёмкостью 5 л в сосуд ёмкостью 12 л
По ссылке http://www.niisi.ru/kumir/ вы можете скачать систему КуМир (Комплект учебных Миров) или скачать архив программы с сайта, в которой используется школьный алгоритмический язык, со встроенными исполнителями Робот, Чертёжник, Водолей и др. Кумир работает в операционных системах Windows и Linux.
Далее, говоря об алгоритмическом языке, мы будем иметь в виду именно школьный алгоритмический язык.
САМОЕ ГЛАВНОЕ
Существуют различные способы записи алгоритмов: словесное описание, построчная запись, блок-схемы, школьный алгоритмический язык и др. Каждый из этих способов обладает своими достоинствами и недостатками.
Вопросы и задания
1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Что вы можете сказать о формах представления информации в презентации и в учебнике? Какими слайдами вы могли бы дополнить презентацию?
2. Каковы основные способы записи алгоритмов?
3. Чем вызвано существование многих способов записи алгоритмов?
4. Дайте словесное описание алгоритма сложения двух обыкновенных дробей а/b и c/d.
5. Представьте в виде построчной записи алгоритм решения следующей задачи: «Имеются четыре арбуза различной массы. Как, пользуясь чашечными весами без гирь, путём не более пяти взвешиваний расположить их по возрастанию веса?».
6. Представьте с помощью блок-схемы алгоритм решения следующей задачи: «Из трёх монет одинакового достоинства одна фальшивая (более лёгкая). Как её найти с помощью одного взвешивания на чашечных весах без гирь?».
7. Запишите на алгоритмическом языке алгоритм построения окружности заданного радиуса r, проходящей через заданные точки А и В.
8. В среде КуМир запишите и выполните алгоритм переливаний (пример 4) для исполнителя Водолей.
9. Подготовьте краткую биографическую справку о Маркове А. А. (младшем).
Электронное приложение к уроку
 |  |  |
| Презентации, плакаты, текстовые файлы | Вернуться к материалам урока | Ресурсы ЭОР |
Cкачать материалы урока
Примеры алгоритмов на естественном языке
Формы записи алгоритмов
На практике наиболее распространены следующие формы представления алгоритмов:
1. Словесный способ записи алгоритма
Словесный способ записи алгоритмов представляет собой описание последовательных этапов обработки данных. Алгоритм задается в произвольном изложении на естественном языке.
Например. Записать алгоритм нахождения наибольшего общего делителя (НОД) двух натуральных чисел (алгоритм Эвклида).
Словесный способ не имеет широкого распространения, так как такие описания:
2. Наибольшее распространение благодаря своей наглядности получил графический способ записи алгоритмов. При графическом представлении алгоритм изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий.
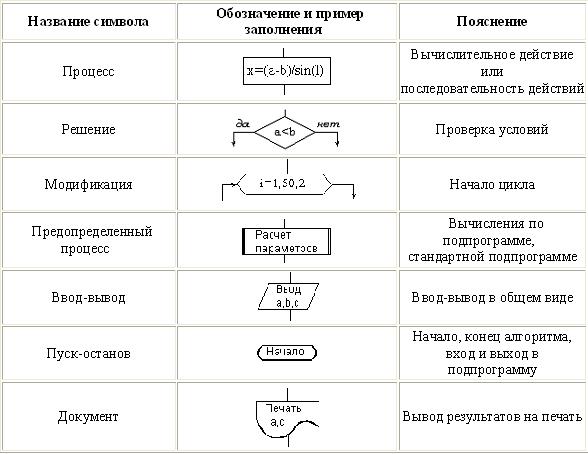
Такое графическое представление называется схемой алгоритма или блок-схемой. В блок-схеме каждому типу действий (вводу исходных данных, вычислению значений выражений, проверке условий, управлению повторением действий, окончанию обработки и т.п.) соответствует геометрическая фигура, представленная в виде блочного символа. Блочные символы соединяются линиями переходов, определяющими очередность выполнения действий. В таблице приведены наиболее часто употребляемые символы.
Блок «процесс» применяется для обозначения действия или последовательности действий, изменяющих значение, форму представления или размещения данных. Для улучшения наглядности схемы несколько отдельных блоков обработки можно объединять в один блок. Представление отдельных операций достаточно свободно.
Блок «решение» используется для обозначения переходов управления по условию. В каждом блоке «решение» должны быть указаны вопрос, условие или сравнение, которые он определяет.
Блок «модификация» используется для организации циклических конструкций. (Слово модификация означает видоизменение, преобразование). Внутри блока записывается параметр цикла, для которого указываются его начальное значение, граничное условие и шаг изменения значения параметра для каждого повторения.
Блок «предопределенный процесс» используется для указания обращений к вспомогательным алгоритмам, существующим автономно в виде некоторых самостоятельных модулей, и для обращений к библиотечным подпрограммам.
Псевдокод представляет собой систему обозначений и правил, предназначенную для единообразной записи алгоритмов.
Псевдокод занимает промежуточное место между естественным и формальным языками. С одной стороны, он близок к обычному естественному языку, поэтому алгоритмы могут на нем записываться и читаться как обычный текст. С другой стороны, в псевдокоде используются некоторые формальные конструкции и математическая символика, что приближает запись алгоритма к общепринятой математической записи.
В псевдокоде не приняты строгие синтаксические правила для записи команд, присущие формальным языкам, что облегчает запись алгоритма на стадии его проектирования и дает возможность использовать более широкий набор команд, рассчитанный на абстрактного исполнителя.
Однако в псевдокоде обычно имеются некоторые конструкции, присущие формальным языкам, что облегчает переход от записи на псевдокоде к записи алгоритма на формальном языке. В частности, в псевдокоде, так же, как и в формальных языках, есть служебные слова, смысл которых определен раз и навсегда. Они выделяются в печатном тексте жирным шрифтом, а в рукописном тексте подчеркиваются.
Единого или формального определения псевдокода не существует, поэтому возможны различные псевдокоды, отличающиеся набором служебных слов и основных (базовых) конструкций.
Информационные технологии копия 2
Основы алгоритмизации и технологии программирования
Понятие алгоритма и его свойства
Каждый из нас постоянно решает множество задач: как быстрее обраться на работу, как лучше спланировать дела текущего дня и многие другие. Некоторые задачи мы решаем автоматически, так как на протяжении многих лет привыкли к их выполнению, другие требуют длительного размышления над решением, но в любом случае, решение каждой задачи всегда делится на простые действия.
Любой алгоритм существует не сам по себе, а предназначен для определенного исполнителя (человека, робота, компьютера, языка программирования и т.д.). Свойством, характеризующим любого исполнителя, является то, что он умеет выполнять некоторые команды. Совокупность команд, которые данный исполнитель умеет выполнять, называется системой команд исполнителя. Алгоритм описывается в командах исполнителя, который будет его реализовывать. Объекты, над которыми исполнитель может совершать действия, образуют так называемую среду исполнителя. Исходные данные и результаты любого алгоритма всегда принадлежат среде того исполнителя, для которого предназначен алгоритм.
Значение слова «алгоритм» очень схоже со значениями слов «рецепт», «метод», «процесс». Однако, в отличие от рецепта или процесса, алгоритм характеризуется следующими свойствами: дискретностью, массовостью, определенностью, результативностью, формальностью.
Дискретность (разрывность – противоположно непрерывности) – это свойство алгоритма, характеризующее его структуру: каждый алгоритм состоит из отдельных законченных действий, говорят: «Делится на шаги».
Массовость – применимость алгоритма ко всем задачам рассматриваемого типа, при любых исходных данных. Например, алгоритм решения квадратного уравнения в области действительных чисел должен содержать все возможные исходы решения, т.е., рассмотрев значения дискриминанта, алгоритм находит либо два различных корня уравнения, либо два равных, либо делает вывод о том, что действительных корней нет.
Определенность (детерминированность, точность) – свойство алгоритма, указывающее на то, что каждый шаг алгоритма должен быть строго определен и не допускать различных толкований; также строго должен быть определен порядок выполнения отдельных шагов. Помните сказку про Ивана-царевича? «Шел Иван-царевич по дороге, дошел до развилки. Видит большой камень, на нем надпись: «Прямо пойдешь – голову потеряешь, направо пойдешь – жену найдешь, налево пойдешь – разбогатеешь. Стоит Иван и думает, что дальше делать». Таких инструкций алгоритм содержать не может.
Результативность – свойство, состоящее в том, что любой алгоритм должен завершаться за конечное (может быть очень большое) число шагов. Вопрос о рассмотрении бесконечных алгоритмов остается за рамками теории алгоритмов.
Формальность – это свойство указывает на то, что любой исполнитель, способный воспринимать и выполнять инструкции алгоритма, действует формально, т.е. отвлекается от содержания поставленной задачи и лишь строго выполняет инструкции. Рассуждать «что, как и почему» должен разработчик алгоритма, а исполнитель формально (не думая) поочередно исполняет предложенные команды и получает необходимый результат.
Способы описания алгоритмов
Рассмотрим следующие способы описания алгоритма: словесное описание, псевдокод, блок-схема, программа.
Словесное описание представляет структуру алгоритма на естественном языке. Например, любой прибор бытовой техники (утюг, электропила, дрель и т.п.) имеет инструкцию по эксплуатации, т.е. словесное описание алгоритма, в соответствии которому данный прибор должен использоваться.
Никаких правил составления словесного описания не существует. Запись алгоритма осуществляется в произвольной форме на естественном, например, русском языке. Этот способ описания не имеет широкого распространения, так как строго не формализуем (под «формальным» понимается то, что описание абсолютно полное и учитывает все возможные ситуации, которые могут возникнуть в ходе решения); допускает неоднозначность толкования при описании некоторых действий; страдает многословностью.
Псевдокод – описание структуры алгоритма на естественном, частично формализованном языке, позволяющее выявить основные этапы решения задачи, перед точной его записью на языке программирования. В псевдокоде используются некоторые формальные конструкции и общепринятая математическая символика.
Строгих синтаксических правил для записи псевдокода не существует. Это облегчает запись алгоритма при проектировании и позволяет описать алгоритм, используя любой набор команд. Однако в псевдокоде обычно используются некоторые конструкции, присущие формальным языкам, что облегчает переход от псевдокода к записи алгоритма на языке программирования. Единого или формального определения псевдокода не существует, поэтому возможны различные псевдокоды, отличающиеся набором используемых слов и конструкций.
Блок-схема – описание структуры алгоритма с помощью геометрических фигур с линиями-связями, показывающими порядок выполнения отдельных инструкций. Этот способ имеет ряд преимуществ. Благодаря наглядности, он обеспечивает «читаемость» алгоритма и явно отображает порядок: выполнения отдельных команд. В блок-схеме каждой формальной конструкции соответствует определенная геометрическая фигура или связанная линиями совокупность фигур.
Рассмотрим некоторые основные конструкции, использующиеся для построения блок-схем (рис. 1).
(1) Блок, характеризующий начало/конец алгоритма (для подпрограмм – вызов/возврат);
(8) Блок – решение (проверка условия или условный блок);
(9) Блок, описывающий блок с параметром;
(10) Блок – границы цикла, описывающий циклические процессы типа: «цикл с предусловием», «цикл с постусловием»;
Описания алгоритма в словесной форме, на псевдокоде или в виде блок-схемы допускают некоторый произвол при изображении команд. Вместе с тем она настолько достаточна, что позволяет человеку понять суть дела и исполнить алгоритм. На практике исполнителями алгоритмов выступают компьютеры. Поэтому алгоритм, предназначенный для исполнения на компьютере, должен быть записан на «понятном» ему языке, такой формализованный язык называют языком программирования.
Программа – описание структуры алгоритма на языке алгоритмического программирования. Программа на языке декларативного программирования представляет собой совокупность описанных знаний и не содержит явного алгоритма исполнения.
Основные алгоритмические конструкции
Элементарные шаги алгоритма можно объединить в следующие алгоритмические конструкции: линейные (последовательные), разветвляющиеся, циклические и рекурсивные.
Линейная алгоритмическая конструкция
Линейной называют алгоритмическую конструкцию, реализованную в виде последовательности действий (шагов), в которой каждое действие (шаг) алгоритма выполняется ровно один раз, причем после каждого i- гo действия (шага) выполняется (i+ 1)-е действие (шаг), если i-e действие – не конец алгоритма.
Опишем алгоритм сложения двух чисел на псевдокоде в виде блок-схемы (рис. 2).
Разветвляющаяся алгоритмическая конструкция
Разветвляющейся (или ветвящейся) называется алгоритмическая конструкция, обеспечивающая выбор между двумя альтернативами в зависимости от значения входных данных. При каждом конкретном наборе входных данных разветвляющийся алгоритм сводится к линейному. Различают неполное (если – то) и полное (если – то – иначе) ветвления. Полное ветвление позволяет организовать две ветви в алгоритме (то или иначе), каждая из которых ведет к общей точке их слияния, так что выполнение алгоритма продолжается независимо от того, какой путь был выбран (рис. 3). Неполное ветвление предполагает наличие некоторых действий алгоритма только на одной ветви (то), вторая ветвь отсутствует, т.е. для одного из результатов проверки никаких действий выполнять не надо, управление сразу переходит к точке слияния (рис. 4).
Рассмотрим стандартный алгоритм поиска наибольшего (наименьшего) значения среди нескольких заданных. Основная идея алгоритма сводится к следующему: за наибольшее (наименьшее) принимаем значение любого из данных. Поочередно сравниваем оставшиеся данные с наибольшим (наименьшим). если окажется, что очередное значение входного данного больше (меньше) наибольшего (наименьшего), то наибольшему (наименьшему) присваиваем это значение. Таким образом, сравнив все входные данные, найдем наибольшее (наименьшее) среди них. Алгоритм использует неполное ветвление.
Заданы три числа. Найти значение наименьшего из них Заданные числа обозначим: а, b, с; результирующее наименьшее – min. На рис. 5 представлена блок-схема алгоритма решения данной задачи.
Алгоритмическая конструкция «Цикл»
Циклической (или циклом) называют алгоритмическую конструкцию, в кoтoрoй некая, идущая подряд группа действий (шагов) алгоритма может выполняться несколько раз, в зависимости от входных данных или условия задачи. Группа повторяющихся действий на каждом шагу цикла называется телом цикла. Любая циклическая конструкция содержит себе элементы ветвящейся алгоритмической конструкции.
Арифметический цикл
В арифметическом цикле число его шагов (повторений) однозначно определяется правилом изменения параметра, которое задается с помощью начального (N) и конечного (К) значений параметра и шагом (h) его изменения. Т.е., на первом шаге цикла значение параметра равно N, на втором – N + h, на третьем – N + 2h и т.д. На последнем шаге цикла значение параметра не больше К, но такое, что дальнейшее его изменение приведет к значению, большему, чем К.
Вывести 10 раз слово «Привет!».
Параметр цикла обозначим i, он будет отвечать за количество выведенных слов. При i=1 будет выведено первое слово, при i=2 будет выведено второе слова и т. д. Так как требуется вывести 10 слов, то последнее значение параметра i=10. В заданном примере требуется 10 раз повторить одно и то же действие: вывести слово «Привет!». Составим алгоритм, используя арифметический цикл, в котором правило изменения параметра i=1,10, 1. т. е. начальное значение параметра i=1; конечное значение i=10; шаг изменения h=1. На рис. 6 представлена блок-схема алгоритма решения данной задачи.
Цикл с предусловием
Количество шагов цикла заранее не определено и зависит от входных данных задачи. В данной циклической структуре сначала проверяется значение условного выражения (условие) перед выполнением очередного шага цикла. Если значение условного выражения истинно, исполняется тело цикла. После чего управление вновь передается проверке условия и т.д. Эти действия повторяются до тех пор, пока условное выражение не примет значение ложь. При первом же несоблюдении условия цикл завершается.
Блок-схема данной конструкции представлена на рис. 7 двумя способами: с помощью условного блока а и с помощью блока границы цикла б. Особенностью цикла с предусловием является то, что если изначально условное выражение ложно, то тело цикла не выполнится ни разу.
Цикл с постусловием
Как и в цикле с предусловием, в циклической конструкции с постусловием заранее не определено число повторений тела цикла, оно зависит от входных данных задачи. В отличие от цикла с предусловием, тело цикла с постусловием всегда будет выполнено хотя бы один раз, после чего проверяется условие. В этой конструкции тело цикла будет выполняться до тех пор, пока значение условного выражения ложно. Как только оно становится истинным, выполнение команды прекращается. Блок-схема данной конструкции представлена на рис. 8 двумя способами: с помощью условного блока а и с помощью блока управления б.
Рекурсивный алгоритм
Рекурсивным называется алгоритм, организованный таким образом, что в процессе выполнения команд на каком-либо шаге он прямо или косвенно обращается сам к себе.
Простые типы данных: переменные и константы
Переменная – есть именованный объект (ячейка памяти), который может изменять свое значение. Имя переменной указывает на зн ачение, а способ ее хранения и адрес остаются скрытыми от программиста. Кроме имени и значения, переменная имеет тип, определяющий, какая информация находится в памяти. Тип переменной задает:
Объем памяти для каждого типа определяется таким образом, чтобы в него можно было поместить любое значение из допустимого диапазона значений данного типа. Например, тип «байт» может принимать значения от О до 255, что в двоичном коде (255(10)=11111111(2)) соответствует ячейке памяти длиной в 8 бит (или 1 байт).
В описанных выше алгоритмах (примеры 1-3) все данные хранятся в виде переменных. Например, инструкция «Ввод двух чисел а, b » означает введение пользователем значений двух переменных, а инструкция «К=К + 1» означает увеличение значения переменной К на единицу.
Если переменные присутствуют в программе, на протяжении всего времени ее работы – их называют статическими. Переменные, создающиеся и уничтожающиеся на разных этапах выполнения программы, называют динамическими.
Все остальные данные в программе, значения которых не изменяются на протяжении ее работы, называют константами или постоянными. Константы, как и переменные, имеют тип. Их можно указывать явно, например, в инструкции «К=К+1» 1 есть константа, или для удобства обозначать идентификаторами: pi=3,1415926536. Только значение pi нельзя изменить, так как это константа, а не переменная.
Структурированные данные и алгоритмы их обработки
Одномерный массив (шкаф ящиков в один ряд) предполагает наличие у каждого элемента только одного индекса. Примерами одномерных массивов служат арифметическая (аi) и геометрическая (bi) последовательности, определяющие конечные ряды чисел. Количество элементов массива называют размерностью. При определении одномерного массива его размерность записывается в круглых скобках, рядом с его именем. Например, если сказано: «задан массив A (10)», это означает, что даны элементы: a 1 , a 2 , …, a 10 . Рассмотрим алгоритмы обработки элементов одномерных массивов.
Ввод элементов одномерного массива осуществляется поэлементно, в порядке, необходимом для решения конкретной задачи. Обычно, когда требуется ввести весь массив, порядок ввода элементов не важен, и элементы вводятся в порядке возрастания их индексов. Алгоритм ввода элементов массива А(10) представлен на рис.9.
В заданном числовом массиве A(l0) найти наибольший элемент и его индекс, при условии, что такой элемент в массиве существует, и единственный.
Обозначим индекс наибольшего элемента т. Будем считать, что первый элемент массива является наибольшим (т = 1). Сравним поочередно наибольший с остальными элементами массива. Если оказывается, что текущий элемент массива а i (тот, c которым идет сравнение) больше выбранного нами наибольшего ат, то считаем его наибольшим (т=i) (рис.10).
Рассмотрим двумерный массив (шкаф с множеством ящиков, положение которых определяется двумя координатами – по горизонтали и по вертикали). В математике двумерный массив (таблица чисел) называется матрицей. Каждый ее элемент имеет два индекса а ij , первый индекс i определяет номер строки, в которой находится элемент (координата по горизонтали), а второй j – номер столбца (координата по вертикали). Двумерный массив характеризуется двумя размерностями N и М, определяющими число строк и столбцов соответственно (рис. 11).
Задана матрица символов (100х100), представляющая собой карту ночного неба; звездам на карте соответствует символы «*». Определить: сколько звезд на карте?
Алгоритм решения задачи достаточно прост, необходимо перебрать все элементы матрицы и посчитать, сколько среди них символов «*». Обозначим К переменную – счетчик. На рис 13. представлена блок-схема решения этой задачи.