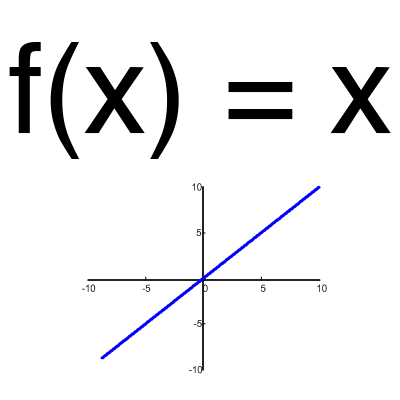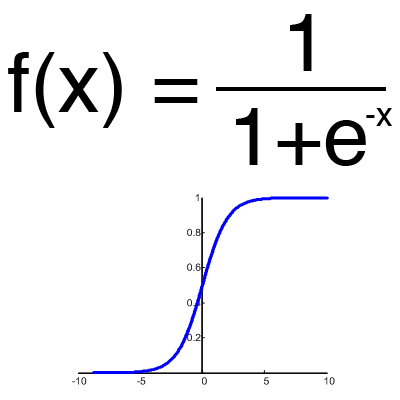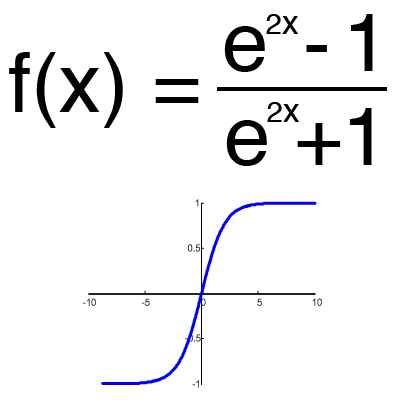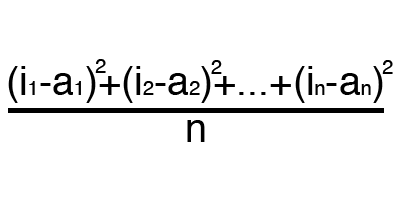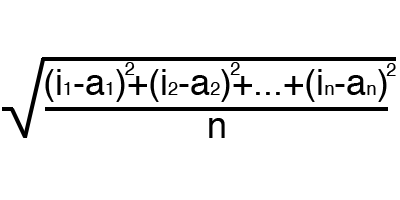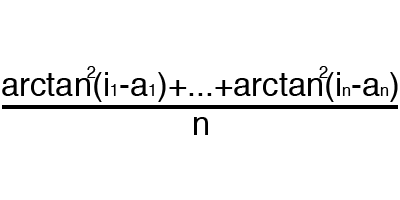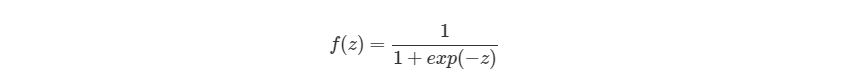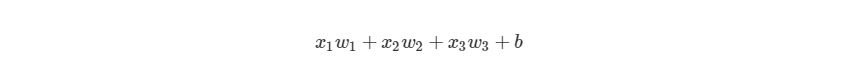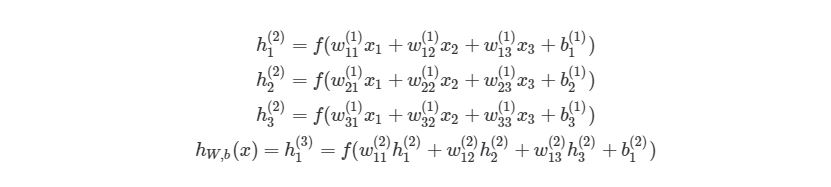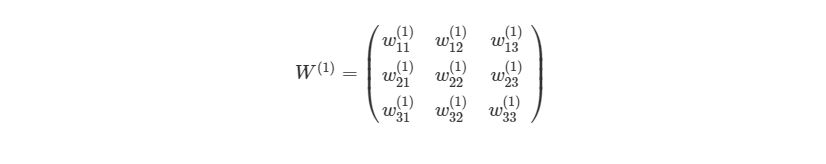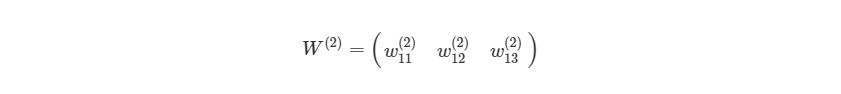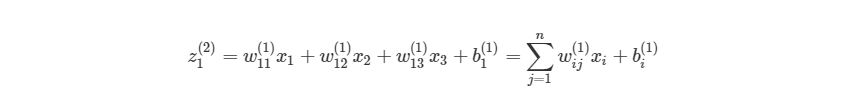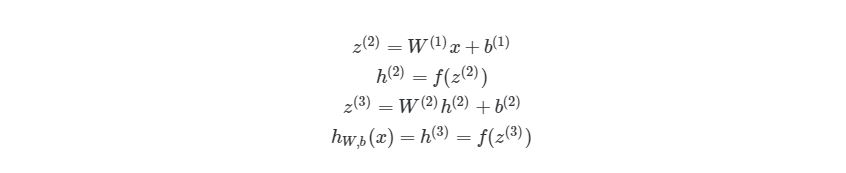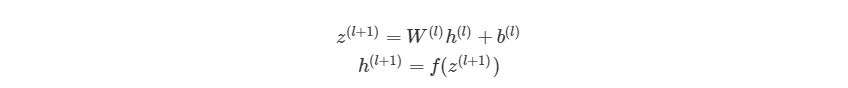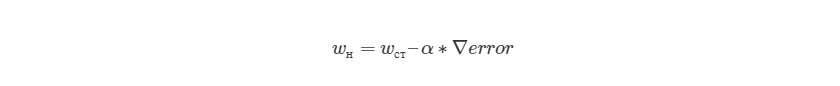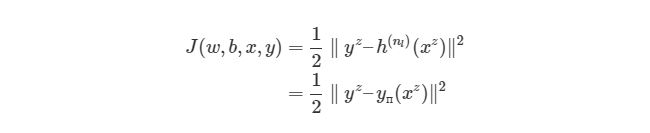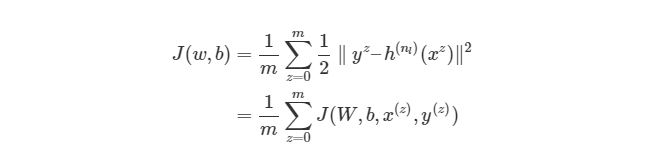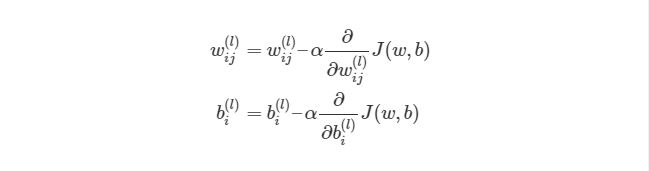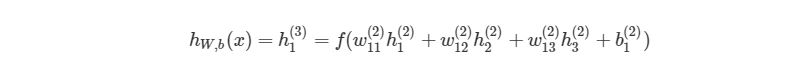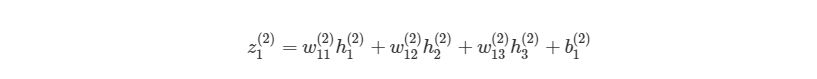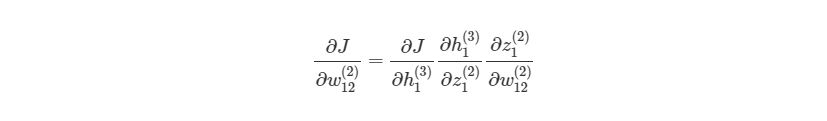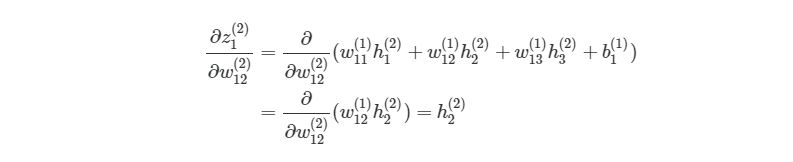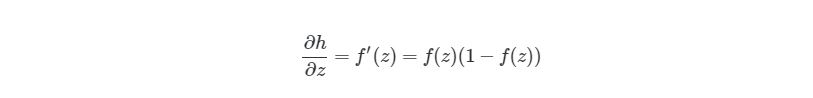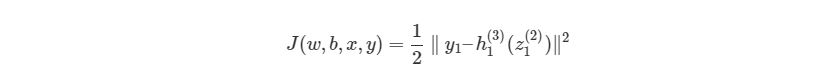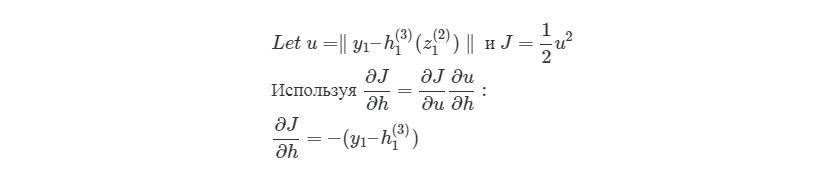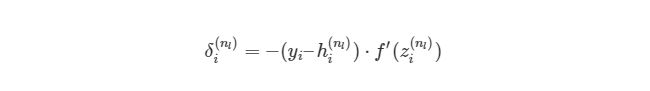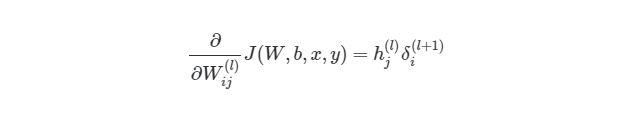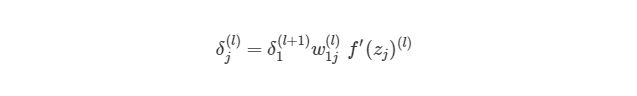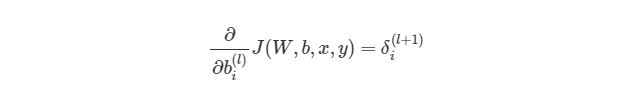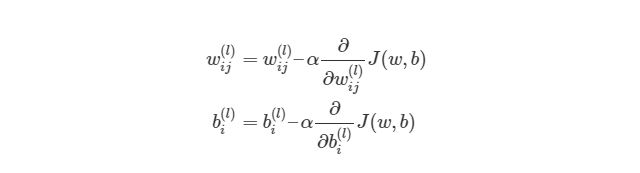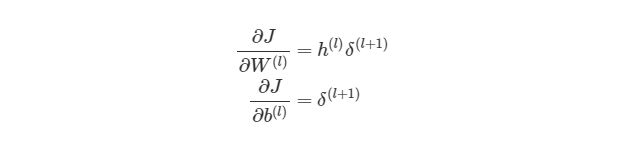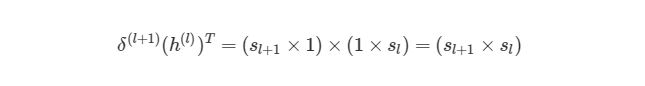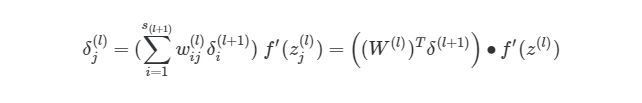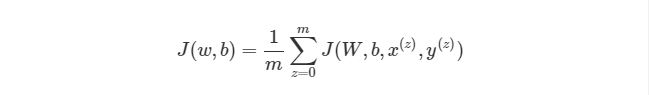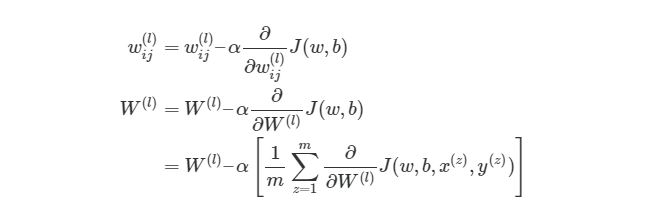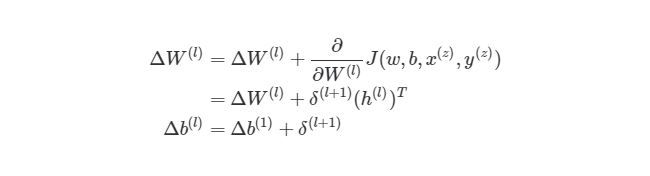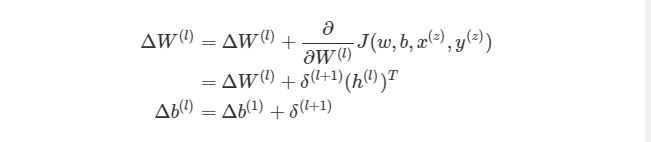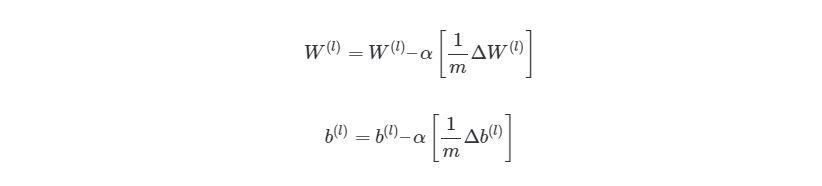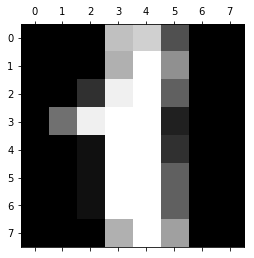Языки программирования для нейросетей
Истинная реализация нейросети с нуля на языке программирования C#
Здравствуй, Хабр! Данная статья предназначена для тех, кто приблизительно шарит в математических принципах работы нейронных сетей и в их сути вообще, поэтому советую ознакомиться с этим перед прочтением. Хоть как-то понять, что происходит можно сначала здесь, потом тут.
Недавно мне пришлось сделать нейросеть для распознавания рукописных цифр(сегодня будет не совсем её код) в рамках школьного проекта, и, естественно, я начал разбираться в этой теме. Посмотрев приблизительно достаточно об этом в интернете, я понял чуть более, чем ничего. Но неожиданно(как это обычно бывает) получилось наткнуться на книгу Саймона Хайкина(не знаю почему раньше не загуглил). И тогда началось потное вкуривание матчасти нейросетей, состоящее из одного матана.
На самом деле, несмотря на обилие математики, она не такая уж и запредельно сложная. Понять сатанистские каракули и письмена этого пособия сможет среднестатистический 11-классник товарищ-физмат или 1
2-курсник технарьского учебного заведения. Помимо этого, пусть книга достаточно объёмная и трудная для восприятия, но вещи, написанные в ней, реально объясняют, что «твориться у тачки под капотом». Как вы поняли я крайне рекомендую(ни в коем случае не рекламирую) «Нейронные сети. Полный курс» Саймона Хайкина к прочтению в том случае, если вам придётся столкнуться с применением/написанием/разработкой нейросетей и прочего подобного stuff’а. Хотя в ней нет материала про новомодные свёрточные сети, никто не мешает загуглить лекции от какого-нибудь харизматичного работника Yandex/Mail.ru/etc. никто не мешает.
Моя видеокарта называется ATI Radeon HD Mobility 4570. И если кто знает, как обратиться к её мощностям для параллелизации нейросетевых вычислений, пожалуйста, напишите в комментарии. Тогда вы поможете мне, и возможно у этой статьи появится продолжение. Не осуждается предложение других ЯП.
Просто, как я понял, она настолько старая, что вообще ничего не поддерживает. Может быть я не прав.
То, что я увидел(третье вообще какая-то эзотерика с некрасивым кодом), несомненно может повергнуть в шок и вас, так как выдаваемое за нейросети связано с ними так же, как и тексты Lil Pump со смыслом. Вскоре я понял, что могу рассчитывать только на себя, и решил написать данную статью, чтобы всякие юзеры не вводили других в заблуждение.
Здесь я не буду рассматривать код сети для распознования цифр(как упоминалось ранее), ибо я оставил его на флэшке, удалив с ноута, а искать сей носитель информации мне лень, и в связи с этим я помогу вам сконструировать многослойный полносвязный персептрон для решения задачи XOR и XAND(XNOR, хз как ещё).
Многослойный полносвязный персептрон.
Один скрытый слой.
4 нейрона в скрытом слое(на этом количестве персептрон сошёлся).
Алгоритм обучения — backpropagation.
Критерий останова — преодоление порогового значения среднеквадратичной ошибки по эпохе.(0.001)
Скорость обучения — 0.1.
Функция активации — логистическая сигмоидальная.

Потом надо осознать, что нам нужно куда-то записывать веса, проводить вычисления, немного дебажить, ну и кортежи поиспользовать. Соответственно, using’и у нас такие.
В папке release||debug этого прожекта располагаются файлы(на каждый слой по одному) по имени типа (fieldname)_memory.xml сами знаете для чего. Они создаются заранее с учётом общего количества весов каждого слоя. Знаю, что XML — это не лучший выбор для парсинга, просто времени было немного на это дело.
Также вычислительные нейроны у нас двух типов: скрытые и выходные. А веса могут считываться или записываться в память. Реализуем сию концепцию двумя перечислениями.
Всё остальное будет происходить внутри пространства имён, которое я назову просто: Neural Network.
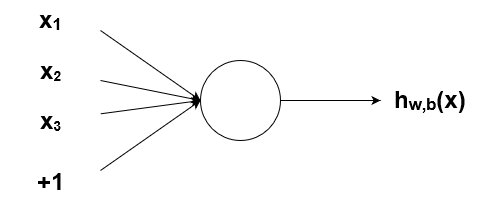
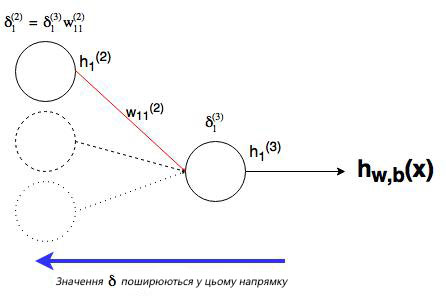
Прежде всего, важно понимать, почему нейроны входного слоя я изобразил квадратами. Ответ прост. Они ничего не вычисляют, а лишь улавливают информацию из внешнего мира, то есть получают сигнал, который будет пропущен через сеть. Вследствие этого, входной слой имеет мало общего с остальными слоями. Вот почему стоит вопрос: делать для него отдельный класс или нет? На самом деле, при обработке изображений, видео, звука стоит его сделать, лишь для размещения логики по преобразованию и нормализации этих данных к виду, подаваемому на вход сети. Вот почему я всё-таки напишу класс InputLayer. В нём находиться обучающая выборка организованная необычной структурой. Первый массив в кортеже — это сигналы-комбинации 1 и 0, а второй массив — это пара результатов этих сигналов после проведения операций XOR и XAND(сначала XOR, потом XAND).
Теперь реализуем самое важное, то без чего ни одна нейронная сеть не станет терминатором, а именно — нейрон. Я не буду использовать смещения, потому что просто не хочу. Нейрон будет напоминать модель МакКаллока-Питтса, но иметь другую функцию активации(не пороговую), методы для вычисления градиентов и производных, свой тип и совмещенные линейные и нелинейные преобразователи. Естественно без конструктора уже не обойтись.
Ладно у нас есть нейроны, но их необходимо объединить в слои для вычислений. Возвращаясь к моей схеме выше, хочу объяснить наличие чёрного пунктира. Он разделяет слои так, чтобы показать, что они содержат. То есть один вычислительный слой содержит нейроны и веса для связи с нейронами предыдущего слоя. Нейроны объединяются массивом, а не списком, так как это менее ресурсоёмко. Веса организованы матрицей(двумерным массивом) размера(нетрудно догадаться) [число нейронов текущего слоя X число нейронов предыдущего слоя]. Естественно, слой инициализирует нейроны, иначе словим null reference. При этом эти слои очень похожи друг на друга, но имеют различия в логике, поэтому скрытые и выходной слои должны быть реализованы наследниками одного базового класса, который кстати оказывается абстрактным.
Класс Layer — это абстрактный класс, поэтому нельзя создавать его экземпляры. Это значит, что наше желание сохранить свойства «слоя» выполняется путём наследования родительского конструктора через ключевое слово base и пустой конструктор наследника в одну строчку(ибо вся логика конструктора определена в базовом классе, и её не надо переписывать).
Теперь непосредственно классы-наследники: Hidden и Output. Сразу два класса в цельном куске кода.
В принципе, всё самое важное я описал в комментариях. У нас есть все компоненты: обучающие и тестовые данные, вычислительные элементы, их «конгламераты». Теперь настало время всё связать обучением. Алгоритм обучения — backpropagation, следовательно критерий останова выбираю я, и выбор мой — есть преодоление порогового значения среднеквадратичной ошибки по эпохе, которое я выбрал равным 0.001. Для поставленной цели я написал класс Network, описывающий состояние сети, которое принимается в качестве параметра многих методов, как вы могли заметить.
Результат обучения.
Итого, путём насилования мозга несложных манипуляций, мы получили основу работающей нейронной сети. Для того, чтобы заставить её делать что-либо другое, достаточно поменять класс InputLayer и подобрать параметры сети для новой задачи.
За сим всё, буду рад ответить на вопросы в комментариях, а пока извольте, новые дела ждут.
P.S.: Для желающих потыкать в код клацать.
UPD1(22.10.2020): господи как давно это было, надеюсь больше не буду писать такие статьи. Скорее всего в то время хотел поделиться с сообществом таким кодом, но так в ML никто не пишет)
Нейронные сети для начинающих. Часть 1
Привет всем читателям Habrahabr, в этой статье я хочу поделиться с Вами моим опытом в изучении нейронных сетей и, как следствие, их реализации, с помощью языка программирования Java, на платформе Android. Мое знакомство с нейронными сетями произошло, когда вышло приложение Prisma. Оно обрабатывает любую фотографию, с помощью нейронных сетей, и воспроизводит ее с нуля, используя выбранный стиль. Заинтересовавшись этим, я бросился искать статьи и «туториалы», в первую очередь, на Хабре. И к моему великому удивлению, я не нашел ни одну статью, которая четко и поэтапно расписывала алгоритм работы нейронных сетей. Информация была разрознена и в ней отсутствовали ключевые моменты. Также, большинство авторов бросается показывать код на том или ином языке программирования, не прибегая к детальным объяснениям.
Поэтому сейчас, когда я достаточно хорошо освоил нейронные сети и нашел огромное количество информации с разных иностранных порталов, я хотел бы поделиться этим с людьми в серии публикаций, где я соберу всю информацию, которая потребуется вам, если вы только начинаете знакомство с нейронными сетями. В этой статье, я не буду делать сильный акцент на Java и буду объяснять все на примерах, чтобы вы сами смогли перенести это на любой, нужный вам язык программирования. В последующих статьях, я расскажу о своем приложении, написанном под андроид, которое предсказывает движение акций или валюты. Иными словами, всех желающих окунуться в мир нейронных сетей и жаждущих простого и доступного изложения информации или просто тех, кто что-то не понял и хочет подтянуть, добро пожаловать под кат.
Первым и самым важным моим открытием был плейлист американского программиста Джеффа Хитона, в котором он подробно и наглядно разбирает принципы работы нейронных сетей и их классификации. После просмотра этого плейлиста, я решил создать свою нейронную сеть, начав с самого простого примера. Вам наверняка известно, что когда ты только начинаешь учить новый язык, первой твоей программой будет Hello World. Это своего рода традиция. В мире машинного обучения тоже есть свой Hello world и это нейросеть решающая проблему исключающего или(XOR). Таблица исключающего или выглядит следующим образом:
| a | b | c |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Соответственно, нейронная сеть берет на вход два числа и должна на выходе дать другое число — ответ. Теперь о самих нейронных сетях.
Что такое нейронная сеть?
Нейронная сеть — это последовательность нейронов, соединенных между собой синапсами. Структура нейронной сети пришла в мир программирования прямиком из биологии. Благодаря такой структуре, машина обретает способность анализировать и даже запоминать различную информацию. Нейронные сети также способны не только анализировать входящую информацию, но и воспроизводить ее из своей памяти. Заинтересовавшимся обязательно к просмотру 2 видео из TED Talks: Видео 1, Видео 2). Другими словами, нейросеть это машинная интерпретация мозга человека, в котором находятся миллионы нейронов передающих информацию в виде электрических импульсов.
Какие бывают нейронные сети?
Пока что мы будем рассматривать примеры на самом базовом типе нейронных сетей — это сеть прямого распространения (далее СПР). Также в последующих статьях я введу больше понятий и расскажу вам о рекуррентных нейронных сетях. СПР как вытекает из названия это сеть с последовательным соединением нейронных слоев, в ней информация всегда идет только в одном направлении.
Для чего нужны нейронные сети?
Нейронные сети используются для решения сложных задач, которые требуют аналитических вычислений подобных тем, что делает человеческий мозг. Самыми распространенными применениями нейронных сетей является:
Классификация — распределение данных по параметрам. Например, на вход дается набор людей и нужно решить, кому из них давать кредит, а кому нет. Эту работу может сделать нейронная сеть, анализируя такую информацию как: возраст, платежеспособность, кредитная история и тд.
Предсказание — возможность предсказывать следующий шаг. Например, рост или падение акций, основываясь на ситуации на фондовом рынке.
Распознавание — в настоящее время, самое широкое применение нейронных сетей. Используется в Google, когда вы ищете фото или в камерах телефонов, когда оно определяет положение вашего лица и выделяет его и многое другое.
Теперь, чтобы понять, как же работают нейронные сети, давайте взглянем на ее составляющие и их параметры.
Что такое нейрон?
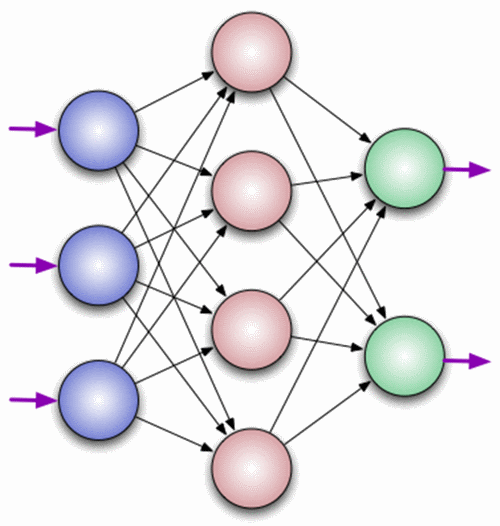
Нейрон — это вычислительная единица, которая получает информацию, производит над ней простые вычисления и передает ее дальше. Они делятся на три основных типа: входной (синий), скрытый (красный) и выходной (зеленый). Также есть нейрон смещения и контекстный нейрон о которых мы поговорим в следующей статье. В том случае, когда нейросеть состоит из большого количества нейронов, вводят термин слоя. Соответственно, есть входной слой, который получает информацию, n скрытых слоев (обычно их не больше 3), которые ее обрабатывают и выходной слой, который выводит результат. У каждого из нейронов есть 2 основных параметра: входные данные (input data) и выходные данные (output data). В случае входного нейрона: input=output. В остальных, в поле input попадает суммарная информация всех нейронов с предыдущего слоя, после чего, она нормализуется, с помощью функции активации (пока что просто представим ее f(x)) и попадает в поле output.
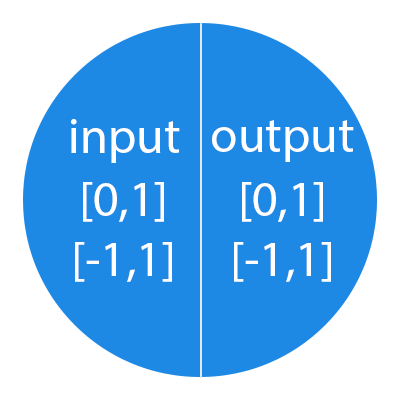
Важно помнить, что нейроны оперируют числами в диапазоне [0,1] или [-1,1]. А как же, вы спросите, тогда обрабатывать числа, которые выходят из данного диапазона? На данном этапе, самый простой ответ — это разделить 1 на это число. Этот процесс называется нормализацией, и он очень часто используется в нейронных сетях. Подробнее об этом чуть позже.
Что такое синапс?
Синапс это связь между двумя нейронами. У синапсов есть 1 параметр — вес. Благодаря ему, входная информация изменяется, когда передается от одного нейрона к другому. Допустим, есть 3 нейрона, которые передают информацию следующему. Тогда у нас есть 3 веса, соответствующие каждому из этих нейронов. У того нейрона, у которого вес будет больше, та информация и будет доминирующей в следующем нейроне (пример — смешение цветов). На самом деле, совокупность весов нейронной сети или матрица весов — это своеобразный мозг всей системы. Именно благодаря этим весам, входная информация обрабатывается и превращается в результат.
Важно помнить, что во время инициализации нейронной сети, веса расставляются в случайном порядке.
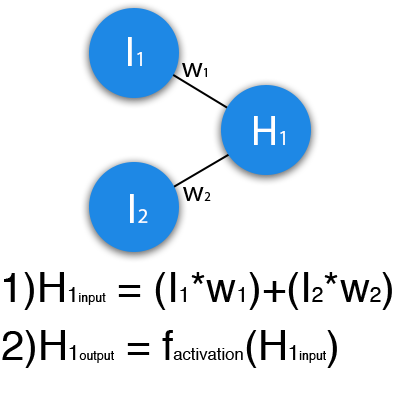
Как работает нейронная сеть?
В данном примере изображена часть нейронной сети, где буквами I обозначены входные нейроны, буквой H — скрытый нейрон, а буквой w — веса. Из формулы видно, что входная информация — это сумма всех входных данных, умноженных на соответствующие им веса. Тогда дадим на вход 1 и 0. Пусть w1=0.4 и w2 = 0.7 Входные данные нейрона Н1 будут следующими: 1*0.4+0*0.7=0.4. Теперь когда у нас есть входные данные, мы можем получить выходные данные, подставив входное значение в функцию активации (подробнее о ней далее). Теперь, когда у нас есть выходные данные, мы передаем их дальше. И так, мы повторяем для всех слоев, пока не дойдем до выходного нейрона. Запустив такую сеть в первый раз мы увидим, что ответ далек от правильно, потому что сеть не натренирована. Чтобы улучшить результаты мы будем ее тренировать. Но прежде чем узнать как это делать, давайте введем несколько терминов и свойств нейронной сети.
Функция активации
Функция активации — это способ нормализации входных данных (мы уже говорили об этом ранее). То есть, если на входе у вас будет большое число, пропустив его через функцию активации, вы получите выход в нужном вам диапазоне. Функций активации достаточно много поэтому мы рассмотрим самые основные: Линейная, Сигмоид (Логистическая) и Гиперболический тангенс. Главные их отличия — это диапазон значений.
Эта функция почти никогда не используется, за исключением случаев, когда нужно протестировать нейронную сеть или передать значение без преобразований.
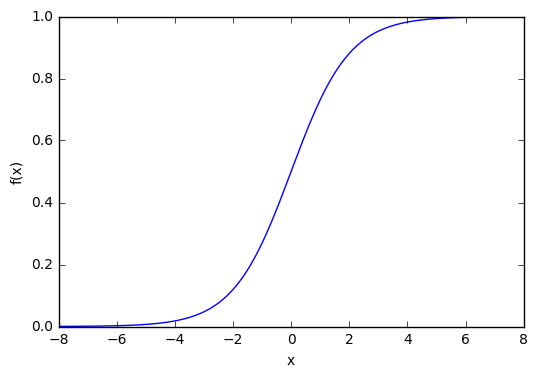
Это самая распространенная функция активации, ее диапазон значений [0,1]. Именно на ней показано большинство примеров в сети, также ее иногда называют логистической функцией. Соответственно, если в вашем случае присутствуют отрицательные значения (например, акции могут идти не только вверх, но и вниз), то вам понадобиться функция которая захватывает и отрицательные значения.
Имеет смысл использовать гиперболический тангенс, только тогда, когда ваши значения могут быть и отрицательными, и положительными, так как диапазон функции [-1,1]. Использовать эту функцию только с положительными значениями нецелесообразно так как это значительно ухудшит результаты вашей нейросети.
Тренировочный сет
Тренировочный сет — это последовательность данных, которыми оперирует нейронная сеть. В нашем случае исключающего или (xor) у нас всего 4 разных исхода то есть у нас будет 4 тренировочных сета: 0xor0=0, 0xor1=1, 1xor0=1,1xor1=0.
Итерация
Это своеобразный счетчик, который увеличивается каждый раз, когда нейронная сеть проходит один тренировочный сет. Другими словами, это общее количество тренировочных сетов пройденных нейронной сетью.
Эпоха
При инициализации нейронной сети эта величина устанавливается в 0 и имеет потолок, задаваемый вручную. Чем больше эпоха, тем лучше натренирована сеть и соответственно, ее результат. Эпоха увеличивается каждый раз, когда мы проходим весь набор тренировочных сетов, в нашем случае, 4 сетов или 4 итераций.
Важно не путать итерацию с эпохой и понимать последовательность их инкремента. Сначала n
раз увеличивается итерация, а потом уже эпоха и никак не наоборот. Другими словами, нельзя сначала тренировать нейросеть только на одном сете, потом на другом и тд. Нужно тренировать каждый сет один раз за эпоху. Так, вы сможете избежать ошибок в вычислениях.
Ошибка
Ошибка — это процентная величина, отражающая расхождение между ожидаемым и полученным ответами. Ошибка формируется каждую эпоху и должна идти на спад. Если этого не происходит, значит, вы что-то делаете не так. Ошибку можно вычислить разными путями, но мы рассмотрим лишь три основных способа: Mean Squared Error (далее MSE), Root MSE и Arctan. Здесь нет какого-либо ограничения на использование, как в функции активации, и вы вольны выбрать любой метод, который будет приносить вам наилучший результат. Стоит лишь учитывать, что каждый метод считает ошибки по разному. У Arctan, ошибка, почти всегда, будет больше, так как он работает по принципу: чем больше разница, тем больше ошибка. У Root MSE будет наименьшая ошибка, поэтому, чаще всего, используют MSE, которая сохраняет баланс в вычислении ошибки.
Принцип подсчета ошибки во всех случаях одинаков. За каждый сет, мы считаем ошибку, отняв от идеального ответа, полученный. Далее, либо возводим в квадрат, либо вычисляем квадратный тангенс из этой разности, после чего полученное число делим на количество сетов.
Задача
Теперь, чтобы проверить себя, подсчитайте результат, данной нейронной сети, используя сигмоид, и ее ошибку, используя MSE.
H1input = 1*0.45+0*-0.12=0.45
H1output = sigmoid(0.45)=0.61
H2input = 1*0.78+0*0.13=0.78
H2output = sigmoid(0.78)=0.69
O1input = 0.61*1.5+0.69*-2.3=-0.672
O1output = sigmoid(-0.672)=0.33
Результат — 0.33, ошибка — 45%.
Большое спасибо за внимание! Надеюсь, что данная статья смогла помочь вам в изучении нейронных сетей. В следующей статье, я расскажу о нейронах смещения и о том, как тренировать нейронную сеть, используя метод обратного распространения и градиентного спуска.
Пишем свою нейросеть: пошаговое руководство
Отличный гайд про нейросеть от теории к практике. Вы узнаете из каких элементов состоит ИНС, как она работает и как ее создать самому.

В этой статье будут представлены некоторые понятия, а также немного кода и математики, с помощью которых вы сможете построить и понять простые нейронные сети. Для ознакомления с материалом нужно иметь базовые знания о матрицах и дифференциалах. Код будет написан на языке программирования Python с использованием библиотеки numpy. Вы построите ИНС, используя Python, которая с высокой точностью классифицировать числа на картинках.
1 Что такое искусственная нейросеть?
Неконтролируемое обучение в ИНС пытается «заставить» ИНС «понять» структуру передаваемой входной информации «самостоятельно». Мы не будем рассматривать это в данном посте.
2 Структура ИНС
2.1 Искусственный нейрон
Которая выглядит следующим образом:
2.2 Узлы
Как было упомянуто ранее, биологические нейроны иерархически соединены в сети, где выход одних нейронов является входом для других нейронов. Мы можем представить такие сети в виде соединенных слоев с узлами. Каждый узел принимает взвешенный вход, активирует активационную функцию для суммы входов и генерирует выход.
Круг на картинке изображает узел. Узел является «местоположением» активационной функции, он принимает взвешенные входы, складывает их, а затем вводит их в активационную функцию. Вывод активационной функции представлен через h. Примечание: в некоторых источниках узел также называют перцептроном.
Что такое «вес»? По весу берутся числа (не бинарные), которые затем умножаются на входе и суммируются в узле. Иными словами, взвешенный вход в узел имеет вид:
где wi— числовые значения веса ( b мы будем обсудим позже). Весы нам нужны, они являются значениями, которые будут меняться в течение процесса обучения. b является весом элемента смещения на 1, включение веса b делает узел гибким. Проще это понять на примере.
2.3 Смещение
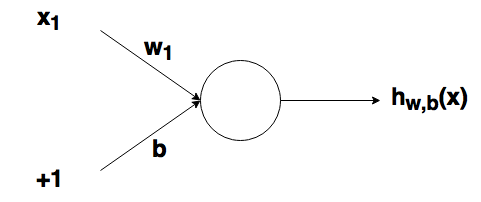
Рассмотрим простой узел, в котором есть по одному входу и выходу:
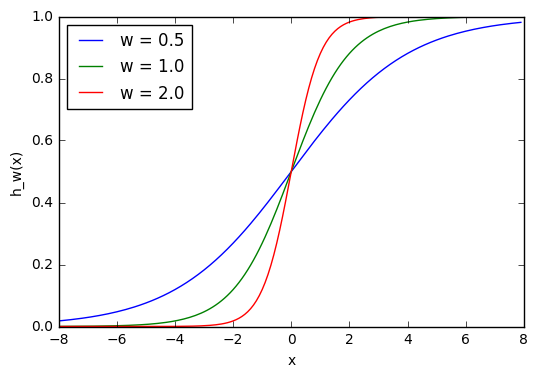
Ввод для активационной функции в этом узле просто x1w1. На что влияет изменение в w1 в этой простой сети?
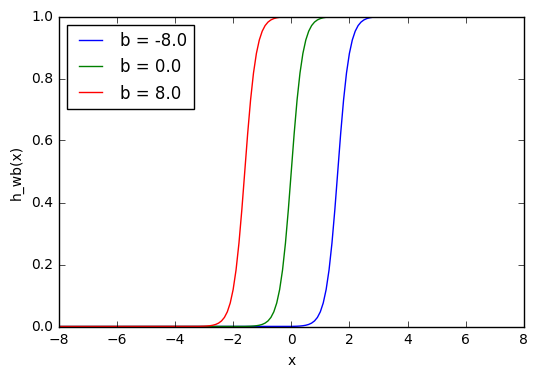
Здесь мы можем видеть, что при изменении веса изменяется также уровень наклона графика активационной функции. Это полезно, если мы моделируем различные плотности взаимосвязей между входами и выходами. Но что делать, если мы хотим, чтобы выход изменялся только при х более 1? Для этого нам нужно смещение. Рассмотрим такую сеть со смещением на входе:
Из графика можно увидеть, что меняя «вес» смещения b, мы можем изменять время запуска узла. Смещение очень важно в случаях, когда нужно имитировать условные отношения.
2.4 Составленная структура
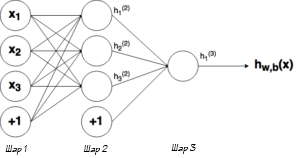
Выше было объяснено, как работает соответствующий узел / нейрон / перцептрон. Но, как вы знаете, в полной нейронной сети находится много таких взаимосвязанных между собой узлов. Структуры таких сетей могут принимать мириады различных форм, но самая распространенная состоит из входного слоя, скрытого слоя и выходного слоя. Пример такой структуры приведены ниже:
2.5 Обозначение
3 Процесс прямого распространения
Чтобы продемонстрировать, как находить выход, имея уже известный вход, в нейронных сетях, начнем с предыдущего примера с тремя слоями. Ниже такая система представлена в виде системы уравнений:
3.1 Пример прямого распространения
Представим эту матрицу через массивы библиотеки numpy.
Мы просто присвоили некоторые рандомные числовые значения весу каждой связи с Ш1. Аналогично можно сделать и с Ш2:
Мы можем присвоить некоторые значения весу смещения в Ш1 и Ш2:
Наконец, перед написанием основной программы для расчета выхода нейронной сети, напишем отдельную функцию для активационной функции:
3.2 Первая попытка реализовать процесс прямого распространения
Приведем простой способ расчета выхода нейронной сети, используя вложенные циклы в Python. Позже мы быстро рассмотрим более эффективные способы.
Функция сначала проверяет, чем является входной массив для соответствующего слоя с узлами / весами. Если рассматривается первый слой, то входом для второго слоя является входной массив xx, Умноженный на соответствующие веса. Если слой не первый, то входом для последующего будет выход предыдущего.
Вызов функции:
возвращает результат 0.8354. Можно проверить правильность, вставив те же значения в систему уравнений:
3.3 Более эффективная реализация
В данном случае процесс прямого распространения с циклами занимает около 40 микросекунд. Это довольно быстро, но не для больших нейронных сетей с > 100 узлами на каждом слое, особенно при их обучении. Если мы запустим этот алгоритм на нейронной сети с четырьмя слоями, то получим результат 70 микросекунд. Эта разница является достаточно значительной.
3.4 Векторизация в нейронных сетях
, где n- количество узлов в Ш1. Используя это обозначение, систему уравнений можно сократить:
Обратите внимание на W, что означает матричную форму представления весов. Помните, что теперь все элементы в уравнении сверху являются матрицами / векторами. Но на этом упрощение не заканчивается. Данные уравнения можно свести к еще более краткому виду:
3.5 Умножение матриц
Распишем z (l+1) =W (l) h (l) +b (l) на выражение из матрицы и векторов входного слоя ( h (l) =x):
Для тех, кто не знает или забыл, как перемножаются матрицы. Когда матрица весов умножается на вектор, каждый элемент в строке матрицы весов умножается на каждый элемент в столбце вектора, после этого все произведения суммируются и создается новый вектор (3х1). После перемножения матрицы на вектор, добавляются элементы из вектора смещения и получается конечный результат.
Каждая строка полученного вектора соответствует аргументу активационной функции в оригинальной НЕ матричной системе уравнений выше. Это означает, что в Python мы можем реализовать все, не используя медленные циклы. К счастью, библиотека numpy дает возможность сделать это достаточно быстро, благодаря функциям-операторам над матрицами. Рассмотрим код простой и быстрой версии функции simple_looped_nn_calc:
Обратите внимание на строку 7, в которой происходит перемножение матрицы и вектора. Если вместо функции умножения a.dot (b) вы используете символ *, то получится нечто похожее на поэлементное умножение вместо настоящего произведения матриц.
Если сравнить время работы этой функции с предыдущей на простой сети с четырьмя слоями, то мы получим результат лишь на 24 микросекунды меньше. Но если увеличить количество узлов в каждом слое до 100-100-50-10, то мы получим гораздо большую разницу. Функция с циклами в этом случае дает результат 41 миллисекунду, когда у функции с векторизацией это занимает лишь 84 микросекунды. Также существуют еще более эффективные реализации операций над матрицами, которые используют пакеты глубинного обучения, такие как TensorFlow и Theano.
На этом все о процессе прямого распространения в нейронных сетях. В следующих разделах мы поговорим о способах обучения нейронных сетей, используя градиентный спуск и обратное распространение.
4 Градиентный спуск и оптимизация
Расчеты значений весов, которые соединяют слои в сети, это как раз то, что мы называем обучением системы. В контролируемом обучении идея заключается в том, чтобы уменьшить погрешность между входом и нужным выходом. Если у нас есть нейросеть с одним выходным слоем и некоторой вход xx и мы хотим, чтобы на выходе было число 2, но сеть выдает 5, то нахождение погрешности выглядит как abs(2-5)=3. Говоря языком математики, мы нашли норму ошибки L 1 (Это будет рассмотрено позже).
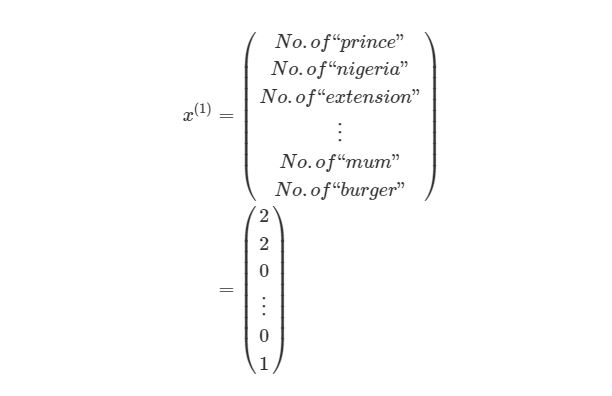
y (1) в этом случае может представлять собой единое скалярное значение, например, 1 или 0, обозначающий, было сообщение спамом или нет. В других приложениях это также может быть вектор с K измерениями. Например, мы имеем вход xx, Который является вектором черно-белых пикселей, считанных с фотографии. При этом y может быть вектором с 26 элементами со значениями 1 или 0, обозначающие, какая буква была изображена на фото, например (1,0. 0)для буквы а, (0,1. 0) для буквы б и т. д.
В обучении сети, используя (x,y), целью является улучшение нахождения правильного y при известном x. Это делается через изменение значений весов, чтобы минимизировать погрешность. Как тогда менять их значение? Для этого нам и понадобится градиентный спуск. Рассмотрим следующий график:
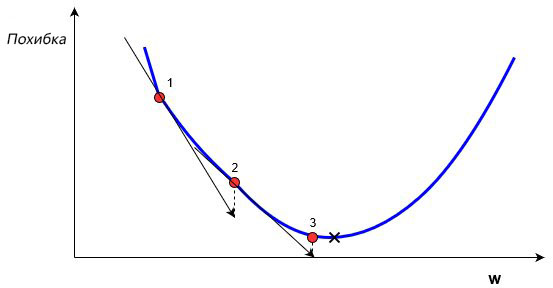
На этом графике изображено погрешность, зависящую от скалярного значения веса, w. Минимально возможная погрешность обозначена черным крестиком, но мы не знаем какое именно значение w дает нам это минимальное значение. Подсчет начинается с рандомного значения переменной w, которая дает погрешность, обозначенную красной точкой под номером «1» на кривой. Нам нужно изменить w таким образом, чтобы достичь минимальной погрешности, черного крестика. Одним из самых распространенных способов является градиентный спуск.
Метод градиентного спуска использует градиент, чтобы принимать решение о следующей смены в w для того, чтобы достичь минимального значения кривой. Он итеративным методом, каждый раз обновляет значение w через:
, где wн означает новое значение w, wст— текущее или «старое» значение w, ∇error является градиентом погрешности на wст и α является шагом. Шаг α также будет означать, как быстро ответ приближается к минимальной погрешности. При каждой итерации в таком алгоритме градиент должен уменьшаться. Из графика выше можно заметить, что с каждым шагом градиент «стихает». Как только ответ достигнет минимального значения, мы уходим из итеративного процесса. Выход можно реализовать способом условия «если погрешность меньше некоторого числа». Это число называют точностью.
4.1 Простой пример на коде
Мы будем находить градиент нейронной сети, используя достаточно популярный метод обратного распространения ошибки, о котором будет написано позже. Но сначала нам нужно рассмотреть функцию погрешности более детально.
4.2 Функция оценки
Выражение является функцией оценки учебного экземпляра zth, где h (nl) является выходом последнего слоя, то есть выход нейронной сети. h (nl) можно представить как yпyп, Что означает полученный результат, когда нам известен вход xz. Две вертикальные линии означают норму L 2 погрешности или сумму квадратов ошибок. Сумма квадратов погрешностей является довольно распространенным способом представления погрешностей в системе машинного обучения. Вместо того, чтобы брать абсолютную погрешность abs(ypred(x z )-y z ), мы берем квадрат погрешности. Мы не будем обсуждать причину этого в данной статье. 1/2 в начале просто константой, которая нормализует ответ после того, как мы продифференцируем функцию оценки во время обратного распространения.
Обратите внимание, что приведенная ранее функция оценки работает только с одной парой (x,y). Мы хотим минимизировать функцию оценки со всеми mm парами вход-выход:
Тогда как же мы будем использовать функцию J для обучения наших сетей? Конечно, используя градиентный спуск и обратное распространение ошибок. Сначала рассмотрим градиентный спуск в нейронных сетях более детально.
4.3 Градиентный спуск в нейронных сетях
Градиентный спуск для каждого веса w(ij) (l) и смещение bi(l) в нейронной сети выглядит следующим образом:
Значения ∂/∂wij (l) и ∂/∂bi (l) являются частными производными функции оценки, основываясь на значениях веса. Что это значит? Вспомните простой пример градиентного спуска ранее, каждый шаг зависит от наклона погрешности / оценки по отношению к весу. Производная также имеет значение наклона / градиента. Конечно, производная обозначается как d/dx. x в нашем случае является вектором, а это значит, что наша производная тоже будет вектором, который является градиент каждого измерения x.
4.4 Пример двумерного градиентного спуска
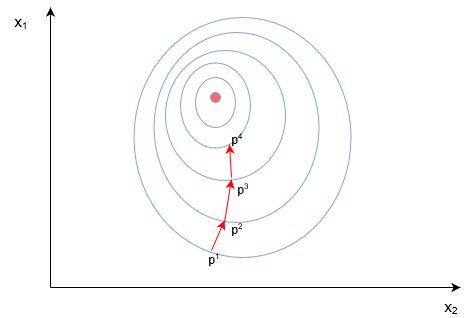
Рассмотрим пример стандартного двумерного градиентного спуска. Ниже представлены диаграмму работы двух итеративных двумерных градиентных спусков:
Синим обозначены контуры функции оценки, они обозначают области, в которых значение погрешности примерно одинаковы. Каждый шаг (p1→p2→p3) В градиентном спуске используют градиент или производную, которые обозначаются стрелкой / вектором. Этот вектор проходит через два пространства [x1, x2][x1,x2]и показывает направление, в котором находится минимум. Например, производная, исчисленная в p1 может быть d/dx=[2.1,0.7], Где производная является вектором с двумя значениями. Частичная производная ∂/∂x1 в этом случае равна скаляру →[2.1]- иными словами, это значение градиента только в одном измерении поискового пространства (x1).
Поэтому нам нужен метод обратного распространения. Этот метод дает нам возможность «делить» функцию оценки или ошибку со всеми весами в сети. Другими словами, мы можем выяснить, как каждый вес влияет на погрешность.
4.5 Углубляемся в обратное распространение
Если математика вам не очень хорошо дается, то вы можете пропустить этот раздел. В следующем разделе вы узнаете, как реализовать обратное распространение языке программирования. Но если вы не против немного больше поговорить о математике, то продолжайте читать, вы получите более глубокие знания по обучению нейронных сетей.
Сначала, давайте вспомним базовые уравнения для нейронной сети с тремя слоями из предыдущих разделов:
Выход этой нейронной сети находится по формуле:
Если присмотреться, то правая часть полностью сокращается (по принципу 2552=22=1). ∂J∂w12(2) были разбиты на три множителя, два из которых можно прекрасно заменить. Начнем с ∂z1 (2) /∂w12 (2) :
здесь y1 является ожидаемым выходом для выходного узла. Опять используем правило дифференцирования сложной функции:
Мы выяснили, как находить ∂J/∂w12 (2) по крайней мере для весов связей с исходным слоем. Перед тем, как перейти к одному из скрытых слоев, введем некоторые новые значения δ, чтобы немного сократить наши выражения:
, где i является номером узла в выходном слое. В нашем примере есть только один узел, поэтому i=1. Напишем полный вид производной функции оценки:
, где выходной слой, в нашем случае, l=2, а i соответствует номеру узла.
4.6 Распространение в скрытых слоях
Что делать с весами в скрытых слоях (в нашем случае в слое 2)? Для весов, которые соединены с выходным слоем, производная ∂J/∂h=-(yi-hi (nl) )имела смысл, т.к. функция оценки может быть сразу найдена через сравнение выходного слоя с существующими данными. Но выходы скрытых узлов не имеют подобных уже существующих данных для проверки, они связаны с функцией оценки только через другие слои узлов. Как мы можем найти изменения в функции оценки из-за изменений весов, которые находятся глубоко в нейронной сети? Как уже было сказано, мы используем метод обратного распространения.
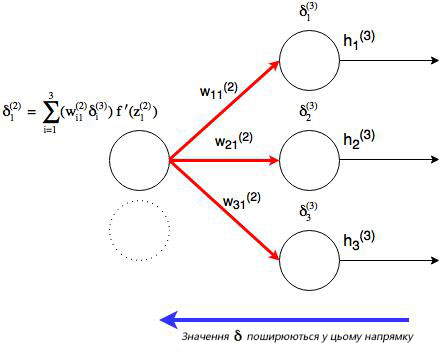
Как можно понять из рисунка, выходной слой соединяется со скрытым узлом из-за веса. В случае, когда в исходном слое есть только один узел, общее выражение скрытого слоя будет выглядеть так:
, где j номер узла в слое l. Но что будет, если в исходном слое находится много выходных узлов? В этом случае δj (l) находится по взвешенной сумме всех связанных между собой погрешностей, как показано на диаграмме ниже:
Отлично, теперь мы знаем, как реализовать градиентный спуск в нейронных сетях:
Однако, для такой реализации, нам нужно будет снова применить циклы. Как мы уже знаем из предыдущих разделов, циклы в языке программирования Python работают довольно медленно. Нам нужно будет понять, как можно векторизовать такие подсчеты.
4.7 Векторизация обратного распространения
Для того, чтобы понять, как векторизовать процесс градиентного спуска в нейронных сетях, рассмотрим сначала упрощенную векторизованную версию градиента функции оценки (внимание: это пока неправильная версия!):
Используя операцию трансформирования, мы можем достичь результата, который нам нужен.
Еще одно трансформирование нужно сделать с суммой погрешностей в обратном распространении:
символ (∙) в предыдущем выражении означает поэлементное умножение (произведение Адамара), не является умножением матриц. Обратите внимание, что произведение матриц (((W (l) ) T δ(l+1))требует еще одного сложения весов и значений δ.
4.8 Реализация этапа градиентного спуска
Как тогда интегрировать векторизацию в этапы градиентного спуска нашего алгоритма? Во-первых, вспомним полный вид нашей функции оценки, который нам нужно сократить:
Из формулы видно, что полная функция оценки состоит из суммы поэтапных расчетов функции оценки. Также следует вспомнить, как находится градиентный спуск (поэлементная и векторизованная версии):
4.9 Конечный алгоритм градиентного спуска
Из этого алгоритма следует, что мы будем повторять градиентный спуск, пока функция оценки не достигнет минимума. На этом этапе нейросеть считается обученной и готовой к использованию.
Далее мы попробуем реализовать этот алгоритм на языке программирования для обучения нейронной сети распознаванию чисел, написанных от руки.
5 Имплементация нейросети языке Python
Код, который мы собираемся написать в нашей нейронной сети, будет анализировать цифры, которые изображают пиксели на изображении. Для начала, нам нужно отсортировать входные данные. Для этого мы сделаем две следующие вещи:
01. Масштабировать данные.
02. Разделить данные на тесты и учебные тесты.
5.1 Масштабирование данных
Почему нам нужно масштабировать данные? Во-первых, рассмотрим представление пикселей одного из сетов данных:
Заметили ли вы, что входные данные меняются в интервале от 0 до 15? Достаточно распространенной практикой является масштабирование входных данных так, чтобы они были только в интервале от [0, 1], или [1, 1]. Это делается для более легкого сравнения различных типов данных в нейронной сети. Масштабирование данных можно легко сделать через библиотеку машинного обучения scikit learn:
5.2 Создание тестов и учебных наборов данных
Опять же, scikit learn легко разбивает данные на учебные и тестовые наборы:
5.3 Настройка выходного слоя
В данных MNIST нужны результаты от изображений записаны как отдельное число. Нам нужно конвертировать это единственное число в вектор, чтобы его можно было сравнивать с исходным слоем с 10 узлами. Иными словами, если результат в MNIST обозначается как «1», то нам нужно его конвертировать в вектор: [0, 1, 0, 0, 0, 0, 0, 0, 0, 0]. Такую конвертацию осуществляет следующий код:
Этот код конвертирует «1» в вектор [0, 1, 0, 0, 0, 0, 0, 0, 0, 0].
5.4 Создаем нейросеть
Мы снова используем сигмоидальную активационную функцию, так что сначала нужно объявить эту функцию и ее производную:
Сейчас мы не имеем никакого представления, как выглядит наша нейросеть. Как мы будем ее учить? Вспомним наш алгоритм из предыдущих разделов:
Рандомно инициализируем веса для каждого слоя W (l) Когда итерация (l) б. Найдите значение δ ( nl) выходного слоя. Обновите ΔW (l) и Δb ( l ) для каждого слоя.
03. Запустите процесс градиентного спуска, используя:
Значит первым этапом является инициализация весов для каждого слоя. Для этого мы используем словари в языке программирования Python (обозначается через <>). Рандомные значения предоставляются весам для того, чтобы убедиться, что нейросеть будет работать правильно во время обучения. Для рандомизации мы используем random_sample из библиотеки numpy. Код выглядит следующим образом:
Следующим шагом является присвоение двум переменным ΔW и Δb нулевых начальных значений (они должны иметь такой же размер, что и матрицы весов и смещений)
Далее запустим процесс прямого распространения через нейронную сеть:
И наконец, найдем выходной слой δ (nl) и значение δ (l) в скрытых слоях для запуска обратного распространения:
Теперь мы можем соединить все этапы в одну функцию:
И наконец, после того, как мы прошлись по всем учебным экземплярам, накапливая значение tri_W и tri_b, мы запускаем градиентный спуск и меняем значения весов и смещений:
После окончания процесса, мы возвращаем полученные вес и смещение со средней оценкой для каждой итерации. Теперь время вызвать функцию. Ее работа может занять несколько минут, в зависимости от компьютера.
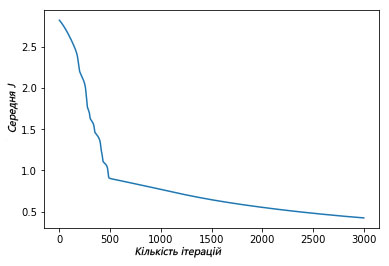
Мы можем увидеть, как функция средней оценки уменьшилась после итерационной работы градиентного спуска:
Выше изображен график, где показано, как за 3000 итераций нашего градиентного спуска функция средней оценки снизилась и маловероятно, что подобная итерация изменит результат.
5.5 Оценка точности модели
Теперь, наконец, мы можем оценить точность результата (процент раз, когда сеть выдала правильный результат), используя функцию accuracy_score из библиотеки scikit learn:
Мы получили результат 86% точности. Звучит довольно неплохо? На самом деле, нет, это довольно низкая точностью. В наше время точность алгоритмов глубинного обучения достигает 99.7%, мы немного отстали.