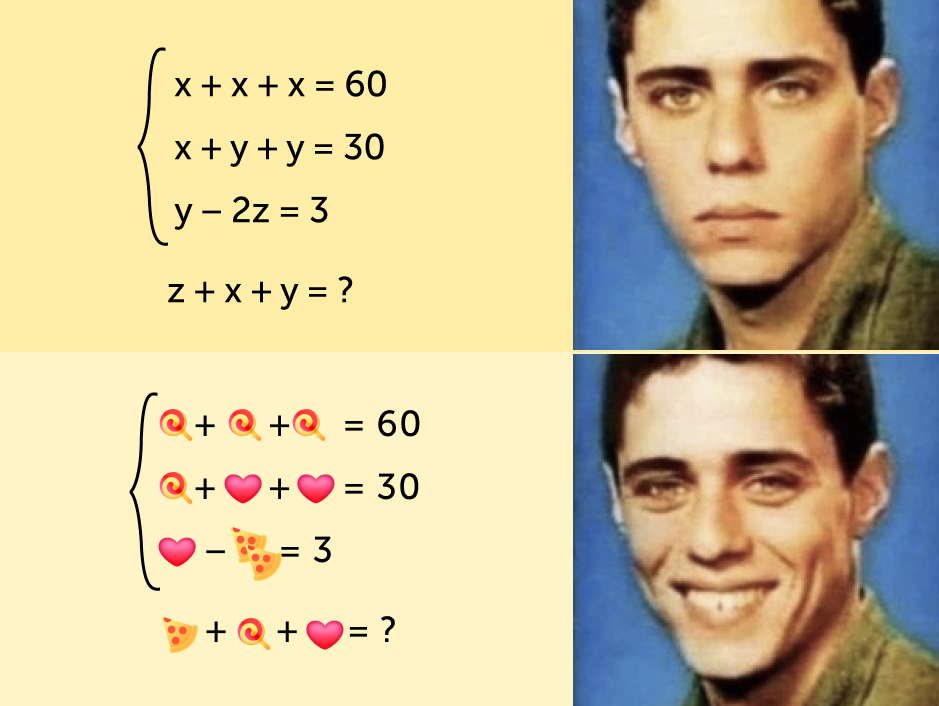Связь математики с иностранными языками
Что общего у английского и математики? 6 неожиданных сходств
Гуманитарии идут на иняз, технари — на матмех. Кажется, всегда было так, а английский и математику разделяла пропасть пошире Ла-Манша. Но если приглядеться, у этих предметов окажется на удивление много общего. Добавляйте свои пункты к нашему списку!
1. И английский, и математика — это языки
С английским все понятно. Но вот к мысли, что математика — тоже язык, нужно привыкнуть.
На самом деле у математики есть главные признаки языка:
2. И английский, и математику понимают по всему миру
Если вы говорите на английском, пусть даже с ошибками и акцентом, вас поймут почти по всему миру. А для математиков и акцент не помеха: китайский школьник может с трудом понимать речь своего индийского сверстника, но когда они начнут разбирать одну и ту же задачу на международной олимпиаде, языковые барьеры исчезнут.
3. И в английском, и в математике есть свои формулы
Времена английского многие учили по формулам, похожим на математические: have + V3, will be + Ving. Английский из-за фиксированного порядка слов вообще гораздо ближе к математике, чем любой другой язык.
4. И в английском, и в математике куча исключений
В математике есть свои неправильные глаголы — например, нельзя делить на ноль и бесконечность. Если такое будет возможно, перестанут работать остальные правила.
В английском, к сожалению, у многих исключений только одно объяснение — «так исторически сложилось». Мир не рухнет, если говорить the goodest, но когда-то люди коллективно согласились, что так неправильно.
5. И английский, и математика гораздо интереснее, чем казалось в школе
Возможно, вы с ужасом вспоминаете «Ландан из зе кэпитал оф Грэйт Британ» и задание «раскройте скобочки». А вот смотреть «Шерлока» в оригинале — совсем другое дело.
С математикой та же история. Задачи про землекопов из школьной программы — тоска и ужас. Но задачки «чему равно сердечко» в соцсетях — это интересный вызов.
Чтобы каждый мог получить удовольствие от изучения математики, мы нарисовали настоящий математический комикс. Там енот отправляется в кругосветное путешествие, а сова и аксолотль (это такой улыбающийся подводный товарищ) ему помогают. Вообще комикс для детей, но мы сами не могли от него оторваться.
6. И английский, и математика дают суперспособности
Предсказывать будущее поможет математика. Если проанализировать данные и построить математическую модель, можно, например, спрогнозировать, сколько новых покупателей придут к вам в следующем месяце.
Прожить вторую жизнь позволяет английский. Для человека, который знает иностранный язык, как будто открывается новое измерение: можно узнавать о событиях в мире, не дожидаясь перевода новостей, путешествовать без страха потеряться и знакомиться с теми, кто никогда не слышал русского.
Закон Зипфа: как связаны математика и быстрое изучение иностранного языка
Лингвистика — это наука, которая требует усидчивости и даже наличия математических способностей. Как связаны графики со словами, и есть ли в мире словарь, который поможет научиться читать на иностранном языке за год?
Американский ученый и педагог Джордж Кингсли Ципф (George Kingsley Zipf; 1902–1950) первым применил в лингвистике статистические методы, то есть «обвенчал» филологию с математикой.
В ходе своей преподавательской работы (Ципф был преподавателем иностранного языка) он, желая повысить эффективность обучения, задумался над совершенствованием методики преподавания. Применяя методы математической статистики к языку, он открыл закон, который впоследствии и был назван в его честь.
Длительное время языкознание считалось гуманитарной наукой. Однако сегодня оно все больше превращается из науки гуманитарной в науку точную, то есть начинает использовать количественные методы, обеспечивающие воспроизводимость результатов исследований и предсказуемость выводов. При этом язык рассматривается, как реально существующий объект, назначение которого – быть средством коммуникации (передачи информации) между людьми.
В чем же смысл закона Зипфа?
Одна из сторон процесса изучения чужого языка — расширение словарного запаса. Хочешь говорить на иностранном языке — учи слова этого языка. Конечно, учить их, читая словарь, что называется, от корки до корки и запоминая все встречающиеся в алфавитном порядке слова, — способ не самый лучший. Одни слова встречаются в языке чаще, а другие реже. Некоторые — совсем редко.
Вы знаете, что такое «тантамареска», и чем она отличается от «тинтамара»? Между тем эти слова входят в словарь русского языка. Правда, они очень редкие. Словарный запас нужно расширять по другому принципу. В первую очередь следует учить наиболее употребительные слова. Таких слов относительно немного — около 2000. Сначала следует осваивать наиболее часто употребляемые в языке слова, потом — слова, которые используются реже, и, наконец, слова, применяемые совсем редко, для украшения и индивидуализации речи.
Если уж и учить иностранные слова по словарю, то словарь этот должен быть не алфавитным, а частотным. В частотном словаре слова располагаются не по алфавиту, а по частоте встречаемости в текстах на изучаемом языке. Например, слово, которое в алфавитном словаре, состоящем из миллиона слов, встретится 100 тысяч раз, в частотном словаре будет стоять раньше слова, частота встречаемости которого 10 тысяч раз на миллион. В свою очередь, это второе слово будет находиться в частотном словаре ближе к началу, чем слово, встречающееся только тысячу раз на миллион слов.
Ципф первый предложил количественную характеристику для больших текстовых массивов: частоту встречаемости слов. Он же вывел закон частотного распределения слов в тексте, справедливый для любого естественного языка. Закон Ципфа определил частотное распределение слов, как универсальную и, вероятно, главную характеристику языка. Очень важно, что частоту распределения слов в языке можно подсчитать, а значит, более или менее однозначно интерпретировать.
Кривая, описывающая закон Зипфа, — гипербола, довольно быстро спадающая и с тянущимся затем почти горизонтальным «хвостом». В спадающей части этой кривой находятся самые употребляемые слова, а в хвосте — слова, употребляемые редко. Зато именно в этой части происходят многие чудеса, благодаря которым в языке появляются новые слова.
Однако во времена Ципфа подсчет частотного распределения слов в языке производился вручную и потому чисто технически был задачей нелегкой. В настоящее время это распределение легко рассчитать на компьютере. Таким образом, компьютер превращается в удобный инструмент, позволяющий производить эксперименты над языком. Первые частотные словари появились относительно недавно. Первый такой словарь английского языка, «The Teacher’s Word Book», вышел в свет в 1921 году. Этот словарь включал 10 тысяч самых употребительных английских слов. В 1944 году он был переиздан в увеличенном объёме (30 тысяч слов). Первый частотный словарь русского языка тоже был издан в США в 1953 году. Он содержал около 5 тысяч слов. Первый частотный словарь современного русского языка появился в 1963 году в Таллине. В нём было представлено две с половиной тысячи наиболее употребительных слов. В 1977 году был издан первый частотный словарь русского языка, который создали с помощью компьютера на базе корпуса текстов в миллион слов.
Интегрированный урок (алгебра + английский язык) «За страницами учебника…», 9 класс.
I. Вступительное слово
Сегодня мы решили провести необычный урок. Урок-экспедицию «За страницами учебника…». Мы будем повторять решение рациональных неравенств и узнаем о выдающихся учёных Великобритании и их вкладе в развитие математики. Во время экспедиции мы будем делать остановки. Результаты вашей работы будут заноситься в маршрутные листы (Рис. 1) и общая оценка за урок будет выставлена, исходя из оценок, полученных на каждом этапе нашего путешествия. Ну а подробнее обо всем вы узнаете из презентации урока.
Маршрутный лист
II. Остановка «Фонетическая-математическая»
Учащиеся произносят за учителем звуки и слова с этими звуками и выполняют задания «верно» – «неверно». Повторение математической лексики.
Фонетическая зарядка. Listen and repeat after me:
Do the sums and comment in English. (слайд № 4)
254 + 71 = 125
124 – 83 = 41
15 * 11 = 165
9.999 : 3 = 3.333
Look at these mathematical signs and say what they mean. (слайд № 4)
III. Остановка « Угадай-ка» (слайды №№ 5 – 11)
Заполните таблицу решений
 |
|
IV. Остановка «Решай устно» (слайды №№ 12,13)
Предлагаем вам устно решить рациональное неравенство по-английски.
V. Остановка «Кто вперёд»
– Рациональные неравенства решаются методом, который позволяет достаточно быстро получить верный ответ, что очень важно при выполнении тестовых заданий на ЕГЭ. Как он называется? (Метод интервалов)
Каждый ученик получает карточку с заданием, в которую нужно вписать решение, графическую иллюстрацию решения неравенств и записать ответ. (Рис.3)
VI. Остановка «Компьютерная»
10 учеников, которые выполнили задания раньше остальных, работают за компьютерами, а остальные в это время выполняют индивидуальные задания на цветных листах. После 10 минут работы ребята, работающие на компьютерах, получают индивидуальные задания (рис.4) [ 2 ], а остальная группа переходит к выполнению тестовых заданий на компьютере (Рис. 5). Используется интерактивное приложение к сборнику «Единый государственный экзамен. Математика. Контрольно-измерительные материалы. 2003–2004. – М.: «Просвещение» [ 4 ].
Примеры заданий компьютерного тестирования


Рис.5
VII. Остановка «Машина времени» (слайды №№ 14–18)
Учитель математики проверяет работы, а учитель английского языка предлагает выполнить задания по чтению.
– Every country is proud of its people who made the country famous and brought it glory. Great Britain is one of such countries. Its outstanding writers and poets, statesmen and politicians, musicians and scientists are well-known all over the world. Now we are going to read about Britain’s famous scientists who made their contribution into mathematics.
Task 1: read the texts and complete the chart.
Task 2: read the texts again and say which two scientists the sentences refer to.
Robert Recorde was born in Tenby, Wales in 1510. Unfortunately we know little about his childhood. As a young adult he studied at Oxford, then at Cambridge where he graduated in medicine. Recorde wrote many books in mathematics. He first used the symbols (+) and (–). Recorde is credited for developing the (=) equal sign. Recorde died in the King’s Bench Prison in 1558, where he was committed for debt [ 5 ].
Isaac Newton, one of the greatest scientists of all times was born in 1642 in a little village in Lincolnshire, England. After school he studied maths at Cambridge University and received his degree in 1665. Newton made three great discoveries – the discoveries of the differential calculuses; the nature of the white light and of the law of gravitation. Newton died at the age of 84 and buried in Westminster Abbey [ 5 ].
Thomas Harriot (1560–1621) was an English scientist and mathematician. He was born in Oxfordshire, England, in 1560. Little is known about his parents. In 1557 Harriot entered the University of Oxford. He studied optics, astronomy and geometry. Thomas Harriot invented the signs for “greater than” (>) and “less than” ( 21.01.2008
«Математика как средство овладения иностранным языком»
МОУ Гимназия № 6 г. Тихорецка
Проблема, над которой работаю:
«Математика как средство овладения иностранным языком».
В нашей стране и родители, и ученики, знают, что математика и иностранный язык являются обязательными предметами в школах любого типа: как в общеобразовательных, так и в специализированных. Почему я, учитель английского языка, вспомнила о математике? Объявления в газетах с предложениями о работе, телереклама нацеливают на обязательное знание иностранного языка, умение работать на компьютере и профессиональной подготовке в выбранной сфере.
Кубань – регион особый. В отдельных уголках нашего края постоянно звучит иноязычная речь (Новороссийск, Анапа, Туапсе, Сочи, Краснодар, Ейск). В школах, расположенных в этих районах, не нужно объяснять необходимость изучения иностранного языка, знакомства с другой культурой.
Совсем иное положение в школах «глубинки» Новопокровского и Тихорецкого районов… Иностранная речь не звучит на улицах города, не востребована на предприятиях. Как же в этих регионах строится обучение иностранным языкам? Что предпочтительнее: математика или английский язык? Оказалось, что это две взаимодополняющие вещи.
Но к проблеме обучения иностранному языку можно подойти по – другому. И такой опыт в нашей стране имеется. Не «язык» ради «языка», а обучение иностранному языку через его прикладные значения.
Уже начиная с 5-го класса у учащихся формируется базовый уровень математики. К Х-ХI классам ученики достигают определенного уровня знаний по этому предмету. У большинства учащихся определяются наклонности к будущей профессии. Часто учащиеся уже приняли решение: кем быть, где учиться дальше. И для тех учащихся, которые выбирали для себя точные, инженерные или экономические науки, проводились факультативные занятия, изучение математики на иностранном языке.
1. На занятиях при объяснении раздела математики использовала только английский язык.
2. Основной учебный материал брала из оригинальных иностранных источников («Mathematics»«text – Pobert Powell, Head of Mathematics
Barton Borough School, Shropshire – design and illustrations – BPP (Letts Educational) Ltd.)
Конечно, во время таких занятий по «математике» использовался уже изученный материал: решение квадратных уравнений на английском языке объясняла учащимся в 9-ом классе ( учащиеся изучают в 8-ом классе.) Но ученики слышали речь на английском языке, как будто они находятся в иностранной языковой среде и формировалась привычка быстрого и непроизвольного использования английского языка, как это происходит на родном языке.
Помня, что математика наука точная и является гимнастикой ума, материал по математике брала из оригинальных иностранных источников, приучала учащихся к краткой и точной формулировке математических терминов на английском языке.
При этом учитывала; что каждый язык имеет свои особенности: идиоматические выражения и термины, которые подчас в области математики невозможно передать методом перевода, т. к. в разных языках нет взаимно однозначных соответствий слов. В данном случае необходимо математическое мышление на английском языке. При таком подходе к изучению английского языка устанавливается нерасторжимая связь между математическим понятием и английским языком.
Из накопленного опыта можно сделать вывод, что я не отвергаю сложившиеся методы обучения английскому языку, а такой подход, когда математика является средством овладения английским языком, только дополняет их. Это позволяет закрепить достигнутый уровень знаний, ещё более заинтересовать учащихся и перейти на другой более высокий уровень.
Конечно, в наших общеобразовательных школах без углубленного обучения английскому языку, не ведется преподавание некоторых предметов на английском языке, но в соответствии с требованиями школьной программы в нашей гимназии № 6 обеспечивается необходимый уровень математики и английского языка. И, чтобы такие уроки проходили успешно, требуется высокий исходный уровень владения математикой и английским языком. Овладение дополнительно лексикой для учащихся не представляет больших трудностей. И, будучи знакомыми с данными разделами математики, без особого труда объясняют как найти корни квадратного уравнения на английском языке, например:
Предлагаю методическую разработку интегрированного урока по теме «Решения квадратных уравнений графическим способом».
Solving Equations Using Graphs.
A quadratics equation is an equation of the form ax2 + bx + c = 0 with a ≠ 0.
You can solve an equation of this form by plotting the graph of y = ax2 + bx + c and finding the value of x when y = 0. This means finding the values of x where the graph crosses the x – axis.
Eg. Solve the equation x2 – x – 2 = 0 by drawing the graph of y = x2 – x – 2
Размышления о взаимодействии лингвистики и математики
Проникновение в лингвистику математических методов и «математического духа» способствовало развитию лингвистики в сторону точности и объективности. Однако на пути ее дальнейшего развития в этом направлении стоят серьезные препятствия. Автор размышляет о причинах сближения лингвистики и математики, о границах применимости в лингвистике математических методов и о природе факторов, препятствующих взаимопониманию математиков и лингвистов.
Когда во второй половине 50-х годов некоторые молодые лингвисты задумались о применении математических методов для исследования структуры языка и начали сотрудничать с математиками, это вызвало у очень многих их коллег удивление и даже шок — ведь они с детства были убеждены, что гуманитарные науки, одной из которых является лингвистика, с математикой и другими «точными» науками не имеют и не могут иметь ничего общего.
Между тем наличие тесной связи между естественным языком и математикой вовсе не было в то время новым открытием. Л. С. Выготский писал в опубликованной в 1934 году книге «Мышление и речь»: «Первым, кто увидел в математике мышление, происходящее из языка, но преодолевающее его, был, по-видимому, Декарт» и продолжал: «Наш обычный разговорный язык из-за присущих ему колебаний и несоответствий грамматического и психологического находится в состоянии подвижного равновесия между идеалами математической и фантастической гармонии и в непрестанном движении, которое мы называем эволюцией».
Возникшее в Древней Греции учение о грамматических категориях уже представляло собой описание ряда важнейших аспектов строения языка с помощью абстрактных моделей, близких по стилю к тем моделям, которые были созданы древнегреческими математиками для описания пространственных форм; только привычность таких понятий, как падеж, род и т. п., ставших, как писал Х. Штейнталь, «нашей второй натурой», мешает нам понять, какого высокого уровня абстрактного мышления потребовало их создание. Так что удивляться следовало бы скорее тому, что первые попытки использовать для описания языкового «идеала математической гармонии» настоящие математические средства были предприняты лишь в середине ХХ столетия.
Можно указать две причины такого «запоздания». Во-первых, наука о языке после значительных шагов, сделанных в античную эпоху, снова начала по-настоящему развиваться только в XIX столетии, но в течение всего этого столетия главное внимание лингвистов было обращено на историю языка, и лишь в следующем веке, который вообще был для гуманитарных наук веком структурализма, лингвистика впервые после античного периода обратилась к изучению языковых структур, но уже на новом уровне. Когда лингвисты осознали, что язык представляет собой, говоря словами Ф. де Соссюра, «систему чистых отношений», т. е. систему знаков, физическая природа которых несущественна, а существенны только отношения между ними, стала совершенно очевидна параллель между языком и математическими конструкциями, которые тоже являются «системами чистых отношений», и уже в начале ХХ столетия тот же де Соссюр мечтал об исследовании языка математическими средствами.
Во-вторых, в математике в начале Нового времени вышли на первый план количественные методы, и только в XIX веке математики снова начали строить неколичественные абстрактные модели, отличавшиеся от античных более высоким уровнем абстракции, а также — что для нашей темы особенно важно — тем, что они могли использоваться для описания значительно более широкого круга явлений, чем пространственные формы; нередко такие модели оказывались удобным и даже необходимым средством для изучения явлений, о которых строившие их математики вовсе не думали и даже не знали об их существовании. Среди этих моделей были и те, которые впоследствии получили применение в лингвистике; особенно интенсивное развитие математических дисциплин, содержанием которых было их построение, пришлось на первую половину ХХ столетия. Поэтому встреча математики и лингвистики в середине этого столетия была вполне закономерна.
Одним из результатов этой встречи было возникновение новой математической дисциплин — математической лингвистики, предметом которой является разработка математического аппарата для лингвистических исследований. Центральное место в математической лингвистике занимает теория формальных грамматик, по характеру используемого в ней аппарата родственная математической логике и в особенности теории алгоритмов. Она доставляет формальные методы описания правильных языковых единиц различных уровней, а также, что особенно важно, формальные методы описания преобразований языковых единиц — как на одном уровне, так и межуровневых. К теории формальных грамматик примыкает теория синтаксических структур, значительно более простая в отношении аппарата, но не менее важная для лингвистических приложений. В математической лингвистике разрабатываются также аналитические модели языка, в которых на основе тех или иных — считающихся известными — данных о «правильных текстах» производятся формальные построения, результатом которых является описание каких-то «составных частей» механизма языка. На этом пути можно получить формальное описание некоторых традиционных грамматических понятий. Сюда же следует отнести описание смысла предложения с помощью аппарата интенсиональной логики («семантику Монтегю»).
Разумеется, с помощью математического аппарата можно описать только один из двух идеалов языка, о которых говорил Выготский; поэтому часто раздающиеся возражения против использования той или иной математической модели (или математических моделей вообще) на том основании, что такие-то и такие-то частные случаи она не охватывает, не имеют смысла: для описания присущих языку «колебаний и несоответствий» нужны совсем другие, не математические средства, и как раз четкое описание «математического идеала» могло бы помочь их находить, поскольку оно позволило бы ясно отграничивать в языке «фантастическое» от «математического». Но это пока что дело будущего.
Не меньшее, а может быть и большее значение, чем возникновение математической лингвистики, имело непосредственное проникновение в лингвистику фундаментальных математических идей и понятий — таких, как множество, функция, изоморфизм. В современной лингвистической семантике важную роль играют пришедшие из математической логики понятия предиката и квантора. (Первое из них возникло в логике еще тогда, когда она не отграничивалась от лингвистики, и теперь вернулось в лингвистику в обобщенном и математически обработанном виде.)
И, наконец, очень большое значение имеет уточнение языка лингвистических исследований, происходящее благодаря проникновению в лингвистику «математического духа» не только в тех ее областях, где возможно использование математических идей и методов. Все это можно коротко резюмировать так: лингвистика становится все более точной и более объективной наукой — не переставая, само собой, быть наукой гуманитарной.
Однако на этом естественном пути развития лингвистики стоят серьезные препятствия, которые могут его надолго затормозить. Главное из них — возникшее в начале Нового времени «разделение факультетов»: естествоиспытатели и математики с одной стороны и гуманитарные ученые с другой не интересуются работой коллег «на другом факультете» и, более того, — в глубине души, а нередко и открыто презирают их. Математики и естествоиспытатели (и еще больше «технари») склонны видеть в гуманитарных исследованиях всего лишь некое «украшение» или даже «пустую болтовню», а «гуманитарии» готовы терпеть математику и естественные науки лишь ради практической пользы и убеждены, что они ничем не могут помочь постижению природы человеческого духа.
Только в середине XIX столетия в этой, говоря словами великого биолога и великого мыслителя Конрада Лоренца, «зловредной стене между естественными и гуманитарными наукам (die böse Mauer zwischen Natur- und Geistwissenschaften)» была пробита первая брешь в самом тонком месте, отделявшем логику от математики. В ХХ столетии появились и другие бреши — среди них и та, которую пробили с двух сторон математики и лингвисты, — но их все еще мало, стена крепка до сих пор, и нет недостатка в усилиях с обеих сторон укреплять ее дальше и латать пробоины. Нередко эти усилия бывают довольно успешны; последнее «достижение» в этом направлении — «профильное образование» в средней школе, уже в детстве разделяющее способных и интересующихся людей на «факультеты» и приучающее их гордиться невежеством в «чужих» науках — может очень сильно воспрепятствовать дальнейшему сближению естественных и гуманитарных наук, настоятельно необходимому для нормального развития тех и других. Одно из последствий воздвижения стены состоит в том, что «гуманитарии», включая подавляющее большинство лингвистов, ничего не знают даже об азах как раз тех разделов математики, которые имеют наибольшее значение для гуманитарных наук (и представляют себе математика как человека, занятого исключительно вычислениями).
Другое препятствие — характерная для нынешнего состояния науки бешеная гонка, безостановочная погоня за все новыми и новыми «результатами», сужающая кругозор и не оставляющая времени задуматься над более глубокими проблемами или заняться серьезным изучением смежной и тем более не совсем смежной научной дисциплины. Это относится в равной степени к лингвистам и к математикам — как, впрочем, и ко всем, кто профессионально занимается наукой.
И третье — инертность, или, проще говоря, лень. На первый взгляд лень и бешеная гонка несовместимы, но в действительности они прекрасно уживаются между собой и, более того, поддерживают и стимулируют друг друга. Когда человеку лень взяться за трудное дело, он хватается за более легкое и более «надежное», успехи в котором оправдывают и поощряют его инертность. Высокомерное отношение к «меньшим братьям», копошащимся по другую сторону стены, также поощряет лень и поощряется ею. Когда, например, математик предлагает пересмотреть все представления о древней истории, не дав себе труда хоть немного познакомиться с древними языками, за это в весьма значительной степени ответственна та же лень-матушка.
Опасность для развития науки, создаваемая этими препятствиями, гораздо серьезнее, чем может показаться на первый взгляд. Когда невежество в «чужих» науках становится предметом гордости, это закономерно ведет к поверхностности и невежеству также и в «своих». «Факультетов» давно уже много больше двух, число их растет из года в год, и каждый отгораживается стеной от других; появляются стены и внутри факультетов. Кругозор исследователей постепенно сужается; правда, аппарат исследования становится все более тонким и изысканным, но в поле его зрения попадают почти исключительно мелкие предметы, и укрепляется представление, будто только они и заслуживают изучения. Есть все основания говорить о кризисе в науке, и лингвистика не является исключением. Сейчас, как мне представляется, самое время оглянуться и задуматься.
Здесь собрались лингвисты того направления, которое связано с моделью «Смысл — Текст». Эта модель, созданная в 60-е годы теперь уже прошлого столетия, была одним из первых и лучших результатов встречи лингвистики и математики, после которой выросли уже два поколения лингвистов, со студенческих лет приучившихся к точному мышлению. Но и они, к сожалению, не свободны от инертности, мешающей им осознать наличие кризиса и задуматься о путях его преодоления. Между тем среди всех лингвистов — и, может быть, даже среди всех, кто занимается гуманитарными науками — у них больше всего объективных возможностей для такого осознания, и хотелось бы надеяться, что они этими возможностями воспользуются.
Текст доклада любезно предоставлен А. В. Гладким и издательством «Языки славянской культуры».