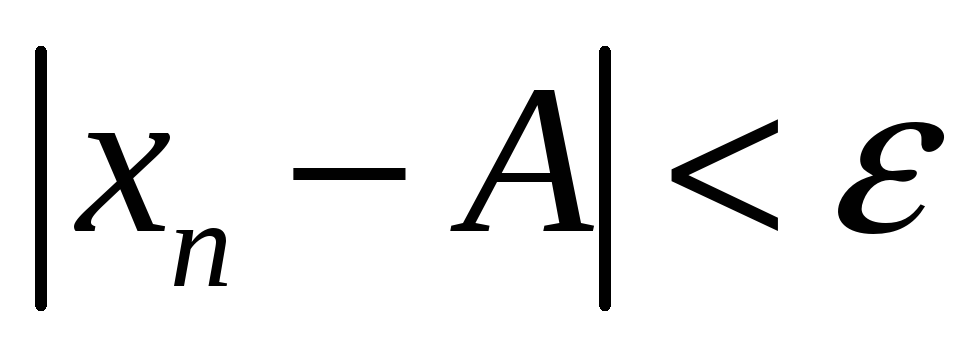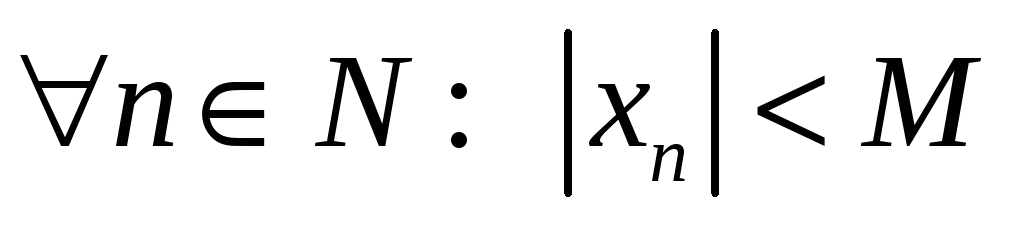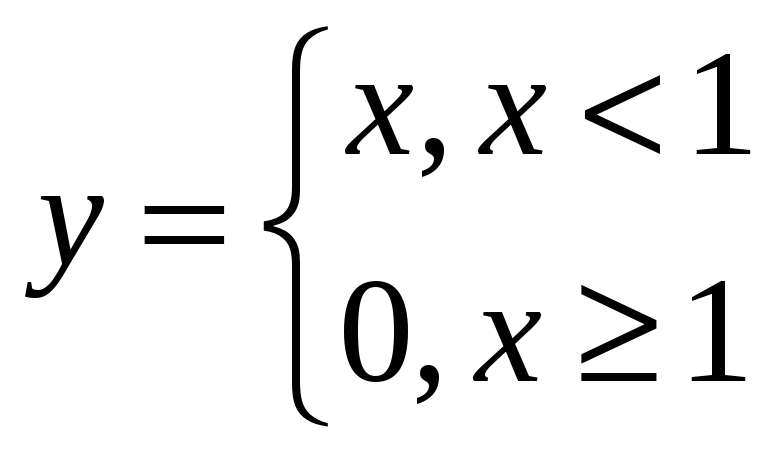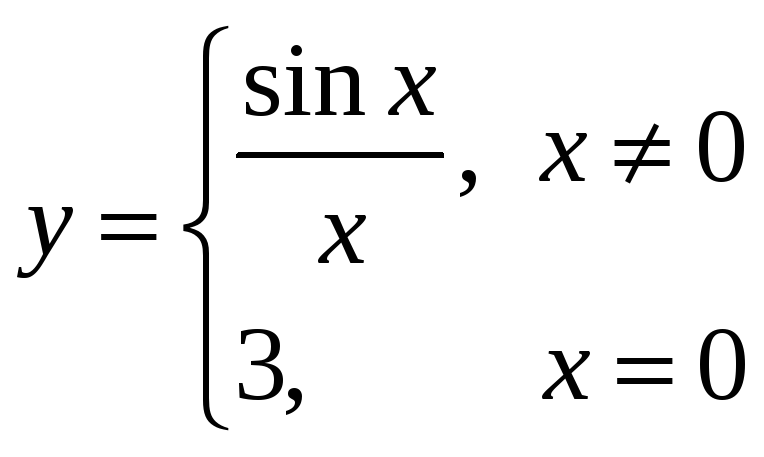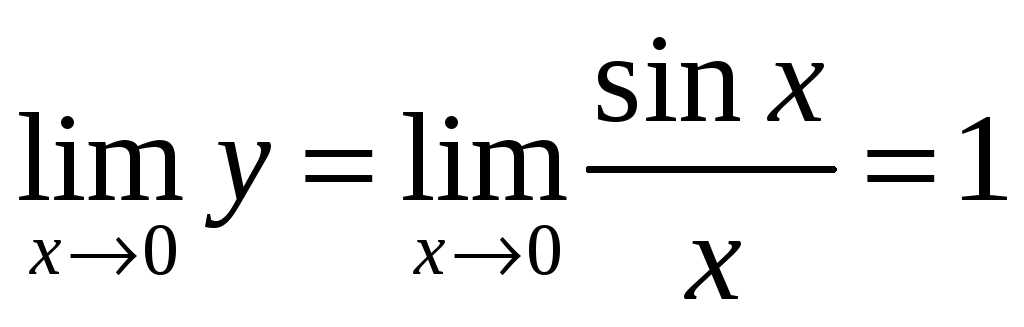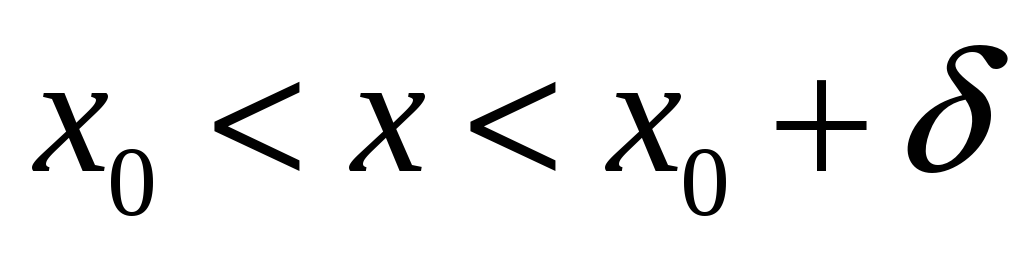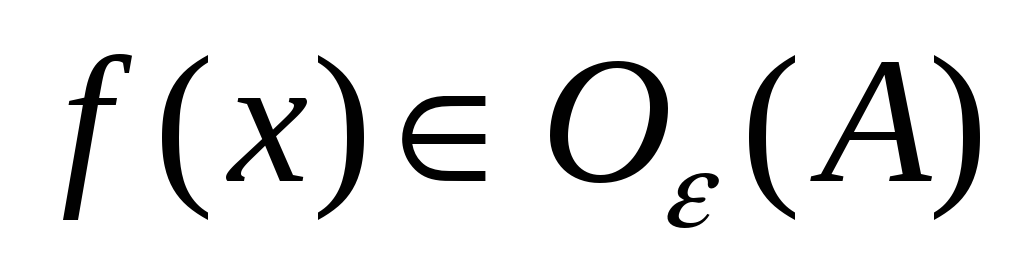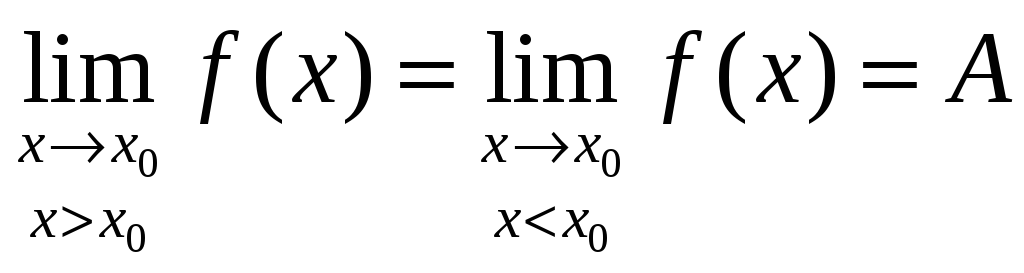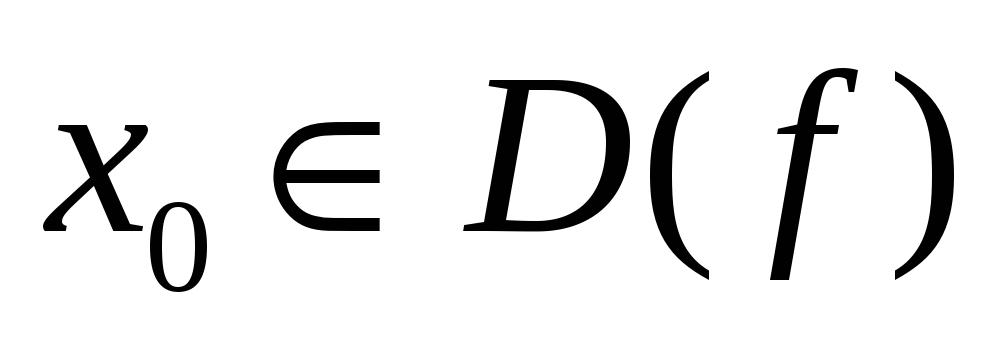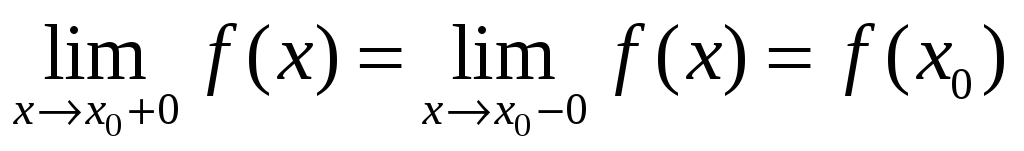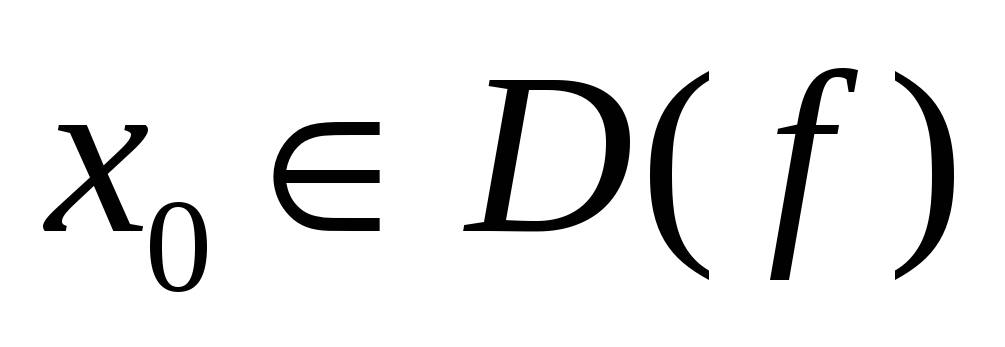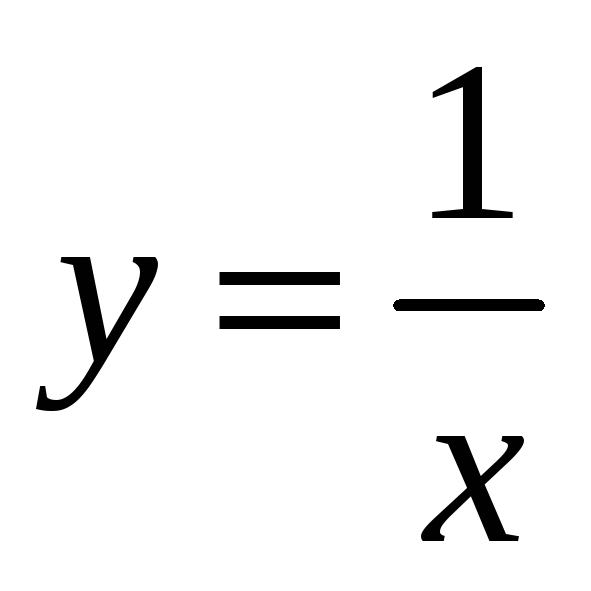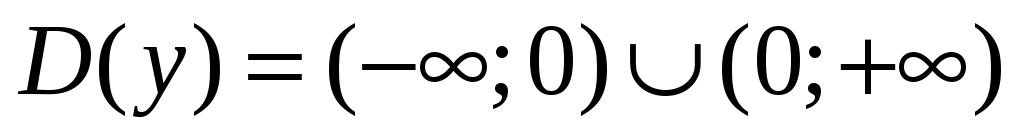Язык эпсилон дельта пределы
Ответы к ГОСу / 5
5. Пределы и непрерывность. Числовая последовательность и ее предел. Определение функции, ее непрерывность на языке «эпсилон-дельта» и языке пределов, равномерная непрерывность.
Если каждому значению n = 1,2,… ставится в соответствие по некоторому закону вещественное число xn, то множество занумерованных вещественных чисел x1, x2,…, xn. = <xn> называется числовой последовательностью. Это частный случай функции, аргумент которой принимает дискретные значеня.
Число A называется пределом последовательности при 
если >0 такой номер N0>0: n > N0: 
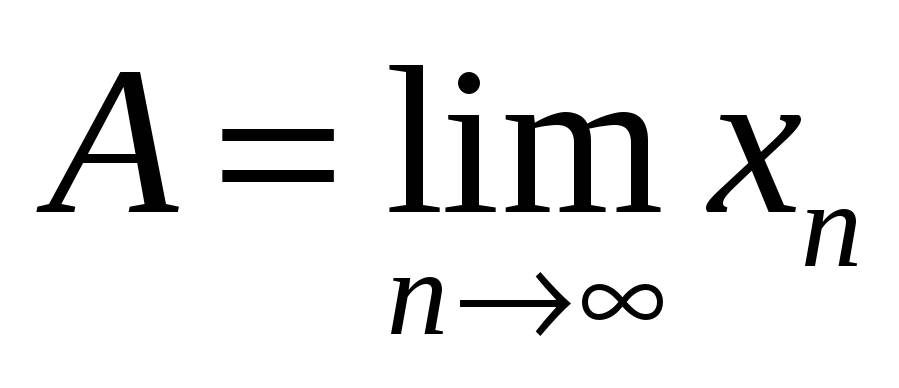
В любой окрестности точки A находятся все члены последовательности, начиная с некоторого номера.
Если существует конечный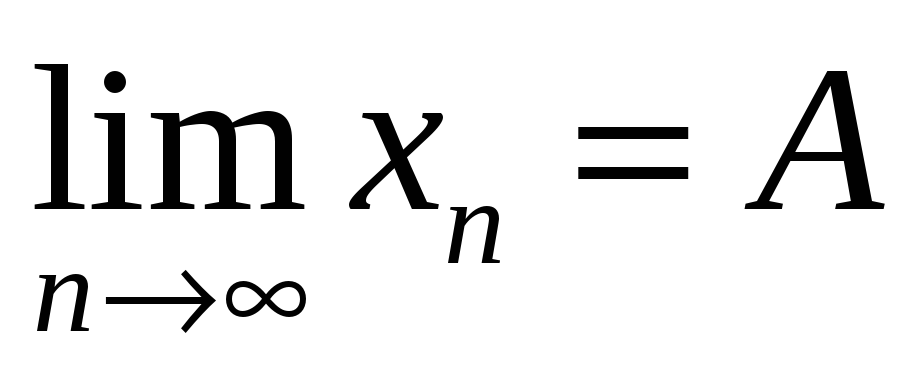 
, то последовательность называется сходящейся. В противном случае (если A = или lim не ) последовательность называется расходящейся.
Точка x0 называется предельной точкой множества M, если в окрестности x0 содержится бесконечное множество точек множества M.
Если последовательность имеет несколько предельных точек, то значение самой большой предельной точки называется верхним пределом последовательности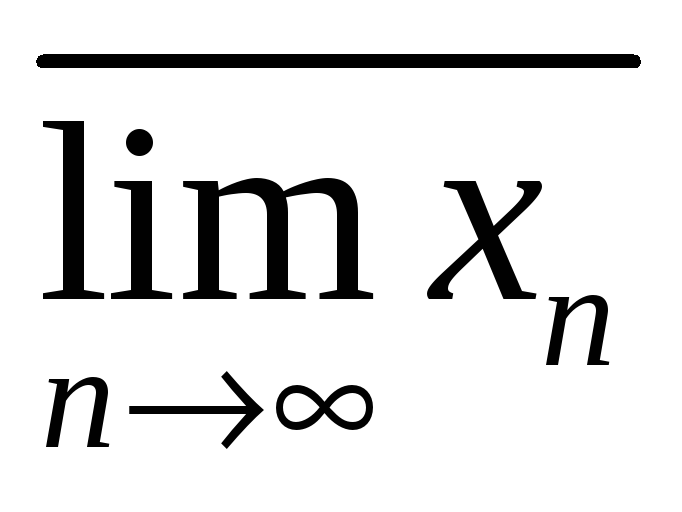 
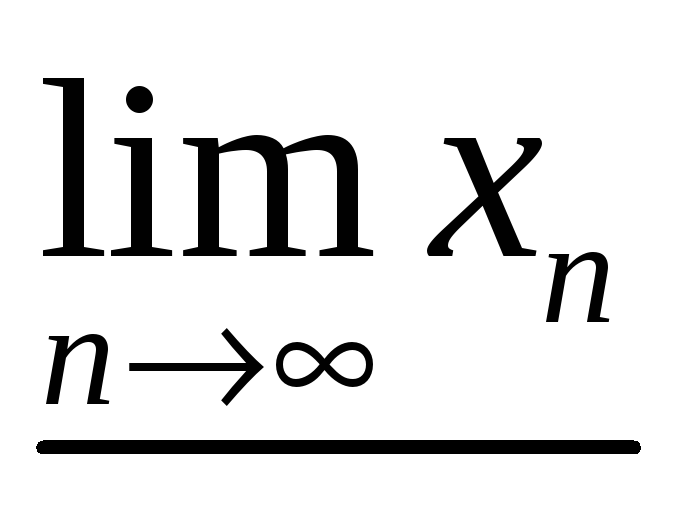
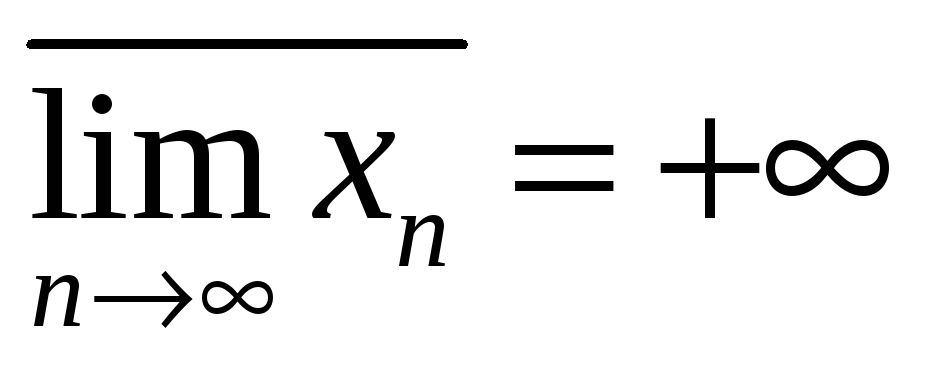
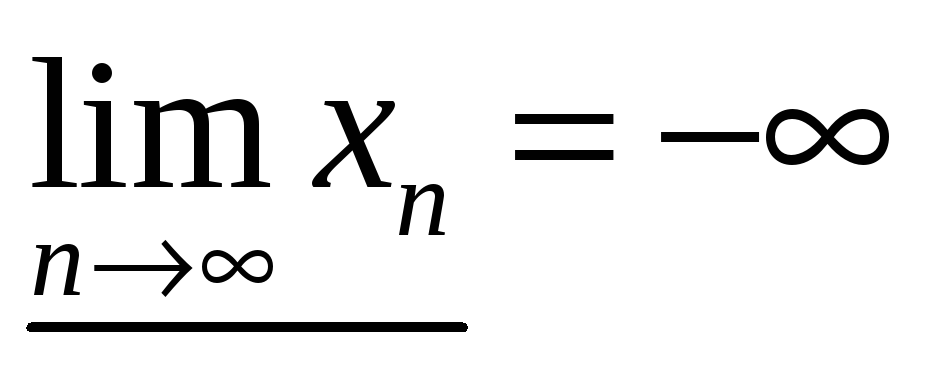
, а значение самой меньшей предельной точки называется нижним пределом последовательности 
.
– неконечный, 
– неконечный.
Последовательность может быть сходящейся, только если она имеет единственную точку (число).
Последовательность называется ограниченной, если M>0, что для 
Т: Из всякой ограниченной последовательности можно выбрать сходящуюся подпоследовательность.
Т: Если последовательность сходится, то она является ограниченной. Обратное неверно.
Но не сходится, так как 2 предельные точки
Если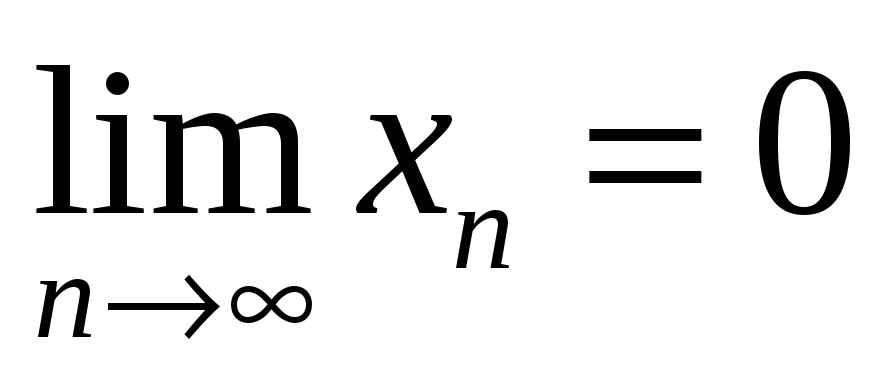 
, то последовательность <xn> называется бесконечно малой.
Если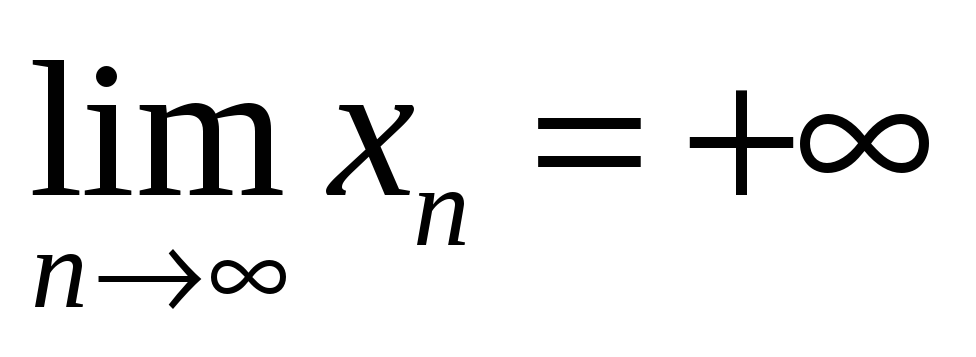 
– бесконечно большой.
Связь неограниченная 
бесконечно большая: бесконечно большая неограниченная
бесконечно большая неограниченная. Обратное не верно:
не бесконечно большая
Функцией y = f(x) называется закон, по которому каждому значению xD(f)R ставится в соответствие единственное действительное число yR.
При этом множество значений аргумента D(f) называется областью определения функции, а множество значений <y | y = f(x), xD(f)> называется множеством значений функции.
Функция может быть задана аналитически (то есть формулой), таблично или графически.
Если функция задана таблично, то чтобы найти значение функции для промежуточных значений аргумента применяют интерполяцию, заменяя функцию линейной, квадратичной на участке между двумя значениями аргумента.
Пусть точка x0 является предельной точкой области определения функции, тогда
для > 0 > 0: xD(f) O(x0) \ <x0>: f(x) O(A)
для > 0 > 0: x: 
для > 0 > 0: x: 
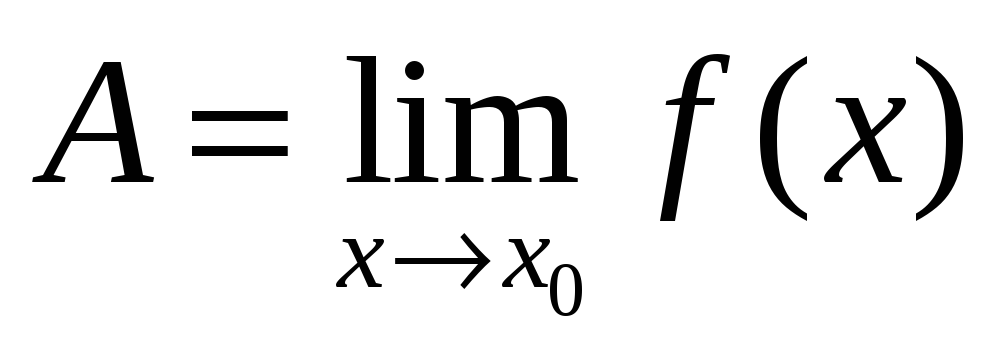
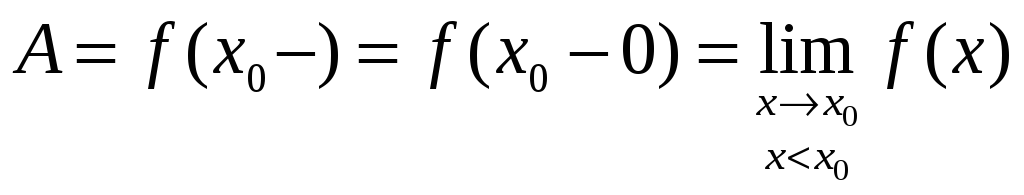
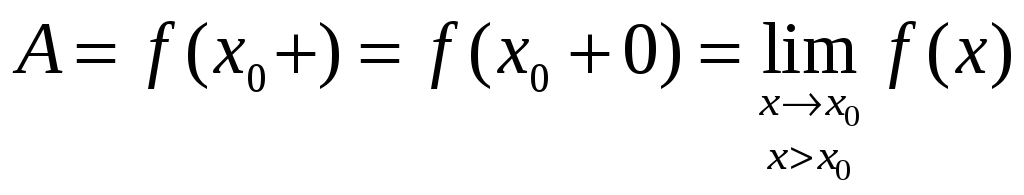
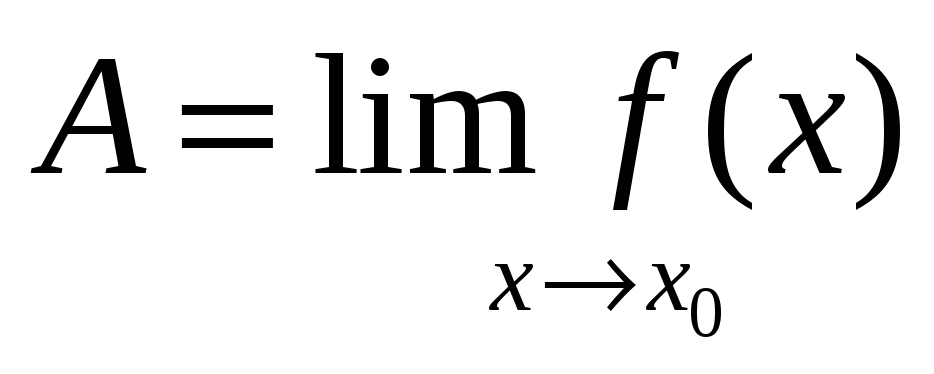
Функция f(x) называется непрерывной в точке x0, если:
.
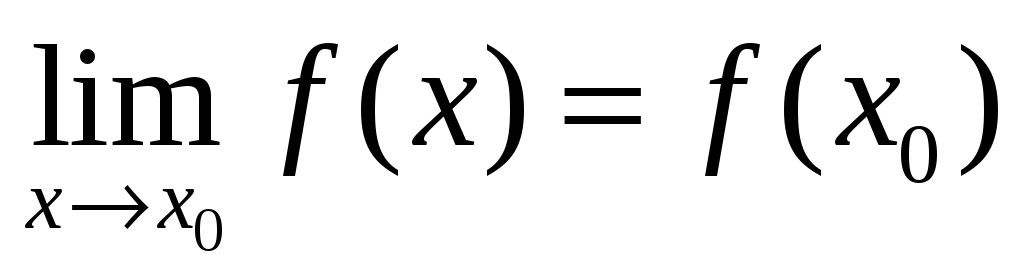
На языке пределов: функция f(x) называется непрерывной в точке x0, если она:
1) определена в этой точке;
2) 
На языке ε и δ: функция f(x) называется непрерывной в точке x0, если:
1) 
1. Если x0 является предельной точкой D(f)
f
(x0+) = A 2 / |x|)
Если функция непрерывна в каждой точке множества X, то она непрерывна на множестве X.
Сумма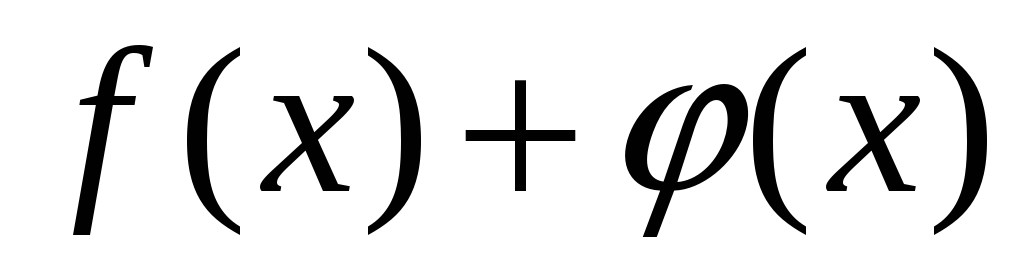 
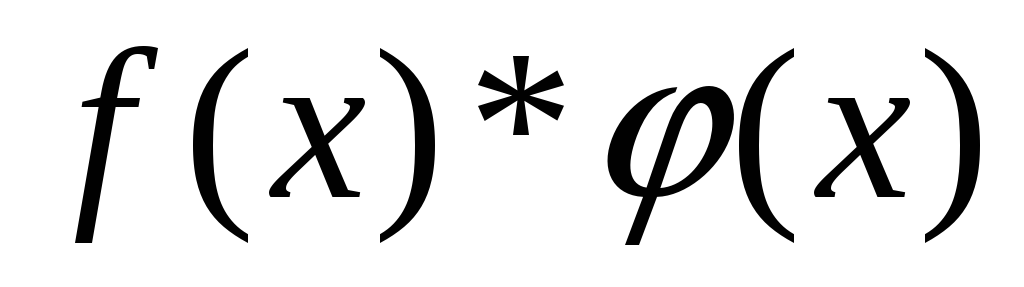
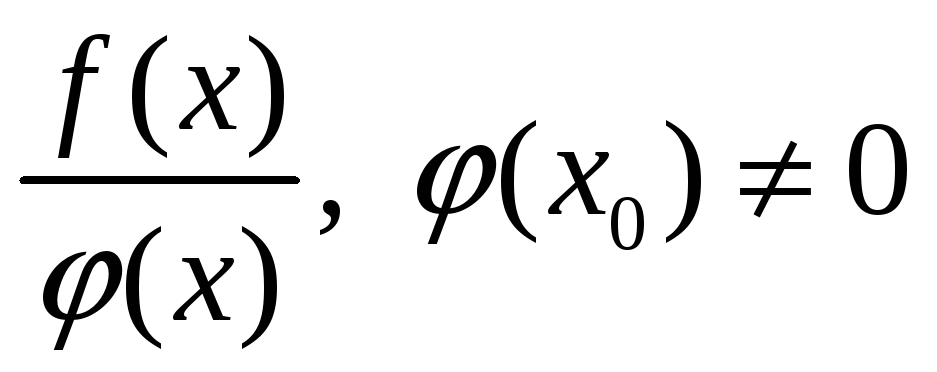
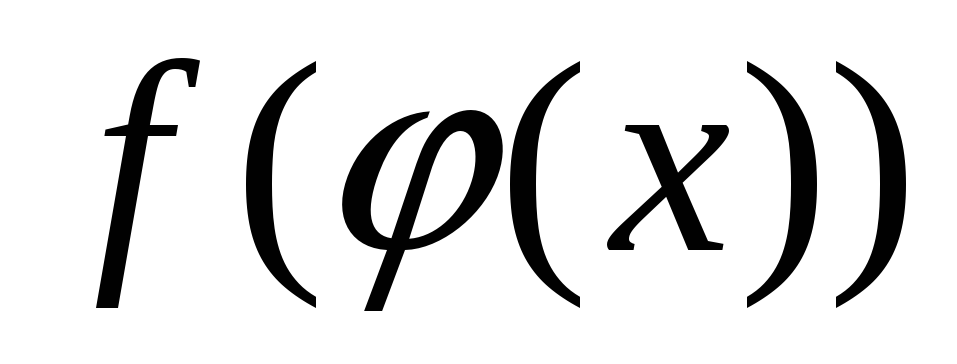
, произведение 
, частное
, суперпозиция 
есть функция непрерывная.
Все элементарные функции непрерывны в своей области определения
Элементарные функции из основных элементарных получаются с помощью конечного числа операций сложения, деления, умножения, суперпозиции.
Исследовать на непрерывность, точки разрыва
Функция элементарна. В своей области определения непрерывна
0 – предельная точка для ОДЗ. Но функция не определена в 0 
это точка разрыва.
– разрыв II рода.
– неэлементарная функция
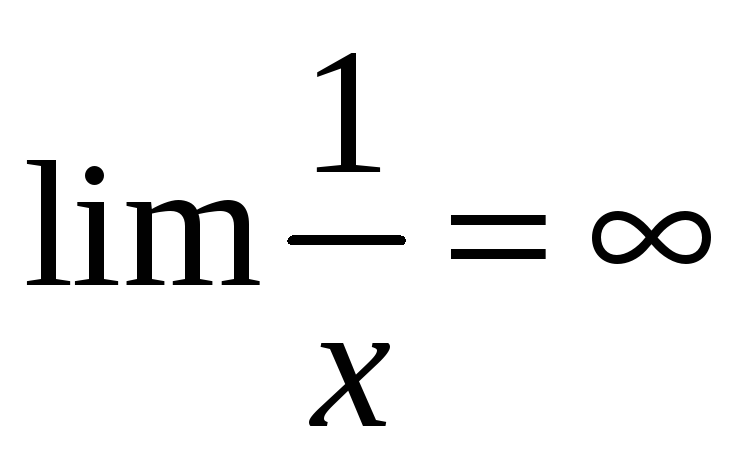
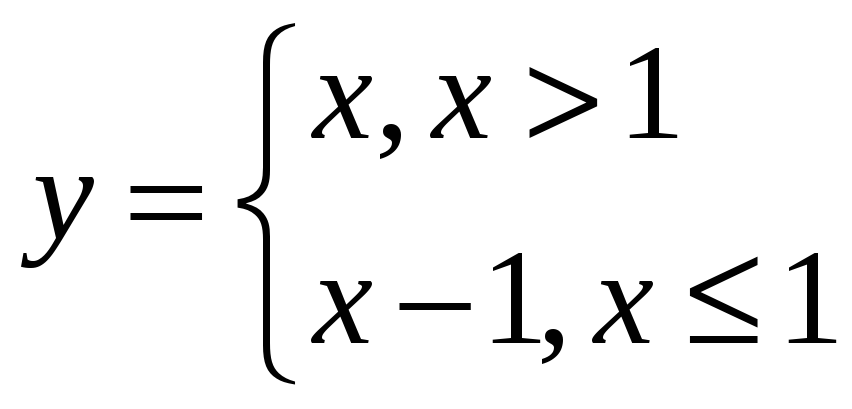
Определение непрерывности функции по Гейне
Функция непрерывна в точке x0, если:
1. она определена в точке x0, то есть 
;
2. для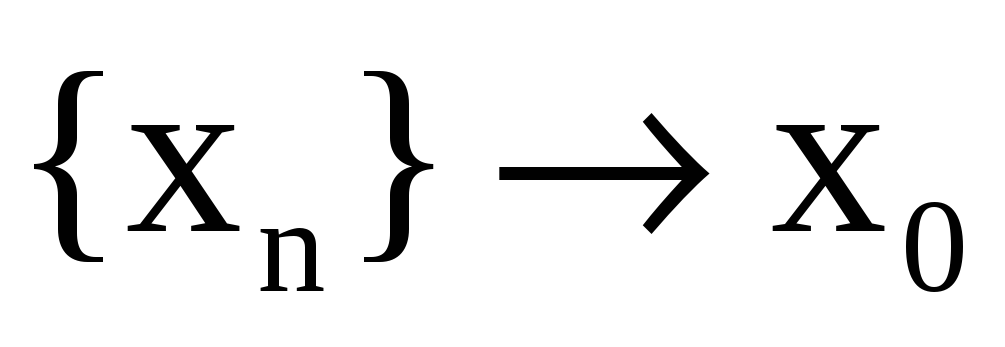 
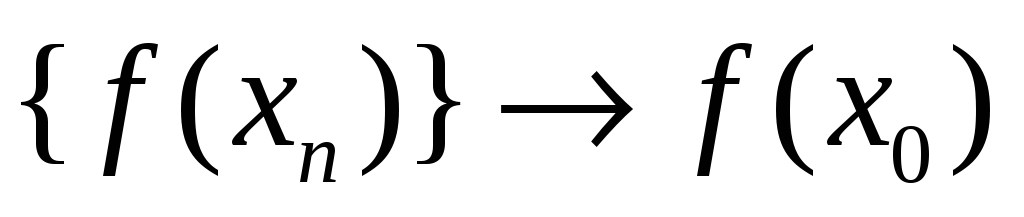
последовательность 
.
Функция Дирихле определена, но разрывна во всех точках
Язык эпсилон дельта пределы
Но я вот еще о чем подумал: к списку примеров в той записи стоит добавить определение предела через эпсилон-дельта. Сейчас, перечитав ее, вижу, что я упомянул его в конце, но только в списке того, что обычно проходят математики в первый год учебы, до теории групп. Этот пример заслуживает отдельного рассмотрения. Всякий, кто преподавал анализ в университете, особенно не студентам-математикам, студентам с других факультетов, знает, как тяжело студентам понять формальное определение предела через эпсилон-дельта, и непосредственно связанные с ним понятия (непрерывность функции, определение производной итд.). Я подумал вдруг, что можно представить это определение в виде некоторой совершенно необходимой ступени на пути к пониманию математики, подобно тому, как Джоэль Спольский предлагает считать понимание указателей и рекурсии (см. ту запись) необходимым шагом на пути к настоящему пониманию программирования. На эту тему есть две интересные заметки Кита Девлина: Letter to a calculus student и Will the real continuous function please stand up? Обе советую, но не буду пытаться их пересказывать, замечу только, что в обоих заметках Девлин рассуждает о том, почему восприятие идей предела и непрерывности оказывается сложным для студентов. В частности, обсуждая понятие предела:
The subtlety that appears to have eluded Bishop Berkeley is that, although we initially think of h as denoting smaller and smaller numbers, the «lim» term in formula (*) asks us to take a leap (and it’s a massive one) to imagine not just calculating quotients infinitely many times, but regarding that entire process as a single entity. It’s actually a breathtaking leap.
А теперь сравним это с тем, что Джоэль Спольский пишет об указателях и рекурсии:
Указатели и рекурсия требуют от человека определённых способностей: рассуждать, абстрактно мыслить, и, что особенно важно, видеть проблему на нескольких уровнях абстракции одновременно.
Не правда ли, похоже? На нескольких уровнях абстракции одновременно. Не в этом ли заключается секрет способности к абстрактному мышлению? Умение держать в уме несколько разных абстрактных понятий, нетривиальным образом между собой связанных (как в случае эпсилон-дельта: для каждого эпсилон существует дельта итд.); умение переходить с одного уровня абстракции на другой, не теряя из виду сами абстрактные понятие и связи между ними.
Пока все; может, еще через неделю еще что-то придумается.
Научный форум dxdy
Математика, Физика, Computer Science, Machine Learning, LaTeX, Механика и Техника, Химия,
Биология и Медицина, Экономика и Финансовая Математика, Гуманитарные науки
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
Определение предела и число эпсилон
 |
1. Предел последовательности.
Цитирую:
2. Геометрический смысл того же предела последовательности:
Заранее благодарен за ответ.
| Заслуженный участник |
 |
| Заслуженный участник |
 |
Последний раз редактировалось ИСН 16.02.2013, 20:14, всего редактировалось 1 раз.
| Заслуженный участник |
 |
| Заслуженный участник |
|
| Заслуженный участник |
|
|
Последний раз редактировалось henehen 16.02.2013, 22:34, всего редактировалось 3 раз(а).
PS. Причём, что самое интересное, такая привычка «объяснять» через левые переменные навроде эпсилонов и дельт сохраняется практически во всех учебниках и методичках, что весьма здорово способствует механическому использованию математики (не вникая ни во что) и убивает напрочь желание учиться.
И вообще, если кто-то мне объяснит человеческим языком на пальцах всю эту эпсилон-дельту технику, то я буду нечеловечески ему благодарен =)
| Заслуженный участник |
|
|
Кто сейчас на конференции
Сейчас этот форум просматривают: нет зарегистрированных пользователей
Ответы к ГОСу / 5
5. Пределы и непрерывность. Числовая последовательность и ее предел. Определение функции, ее непрерывность на языке «эпсилон-дельта» и языке пределов, равномерная непрерывность.
Если каждому значению n = 1,2,… ставится в соответствие по некоторому закону вещественное число xn, то множество занумерованных вещественных чисел x1, x2,…, xn. = <xn> называется числовой последовательностью. Это частный случай функции, аргумент которой принимает дискретные значеня.
Число A называется пределом последовательности при
если >0 такой номер N0>0: n > N0:
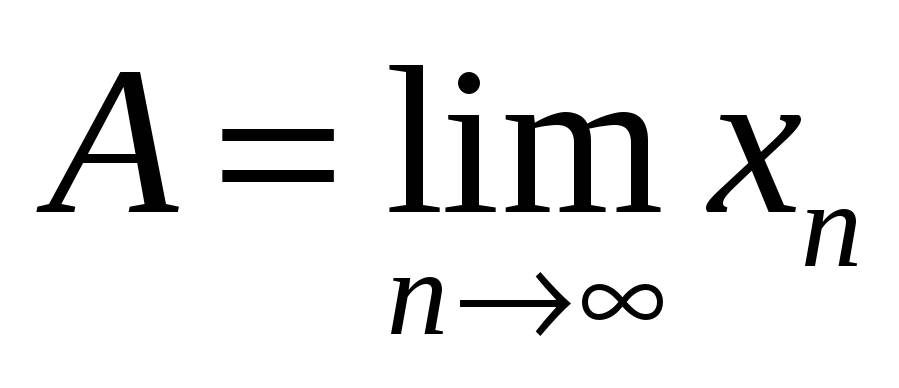
В любой окрестности точки A находятся все члены последовательности, начиная с некоторого номера.
Если существует конечный 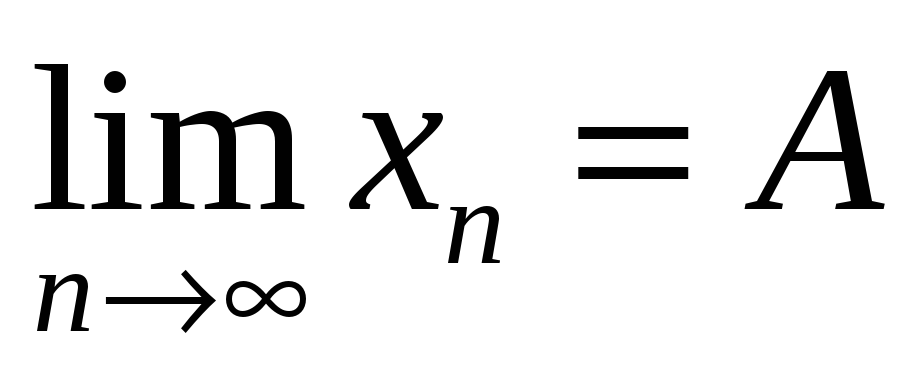, то последовательность называется сходящейся. В противном случае (если A = или lim не ) последовательность называется расходящейся.
Точка x0 называется предельной точкой множества M, если в окрестности x0 содержится бесконечное множество точек множества M.
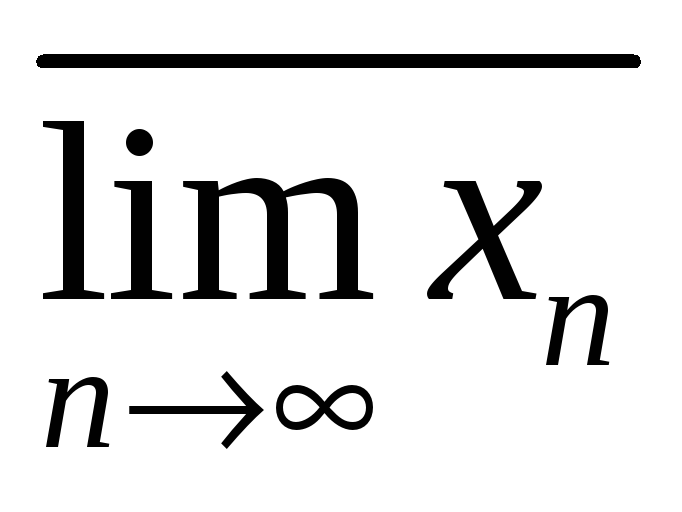
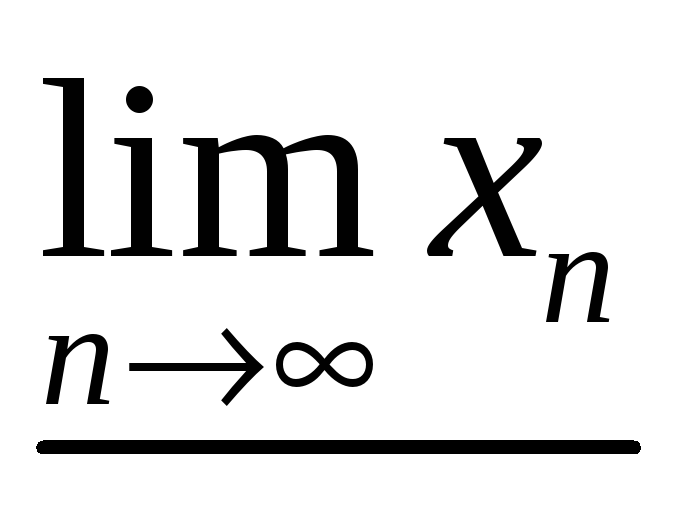
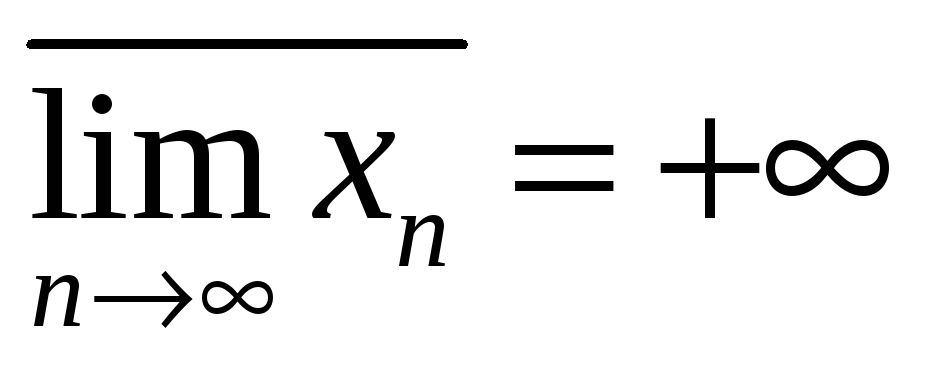
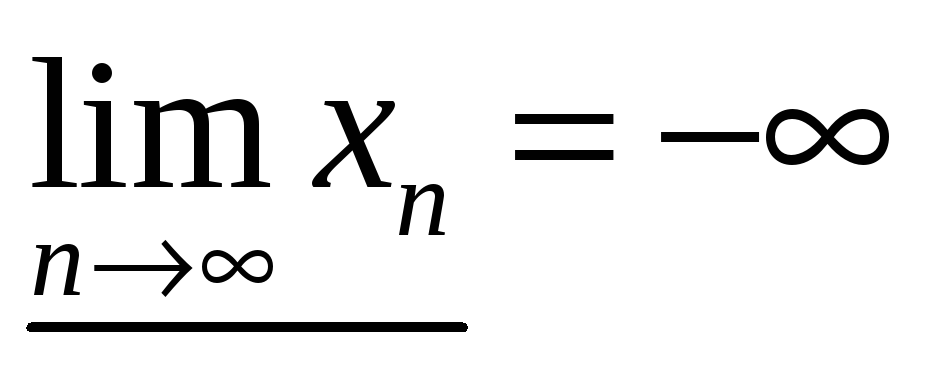
Если последовательность имеет несколько предельных точек, то значение самой большой предельной точки называется верхним пределом последовательности , а значение самой меньшей предельной точки называется нижним пределом последовательности .
– неконечный, – неконечный.
Последовательность может быть сходящейся, только если она имеет единственную точку (число).
Последовательность называется ограниченной, если M>0, что для
Т: Из всякой ограниченной последовательности можно выбрать сходящуюся подпоследовательность.
Т: Если последовательность сходится, то она является ограниченной. Обратное неверно.
Но не сходится, так как 2 предельные точки
Если 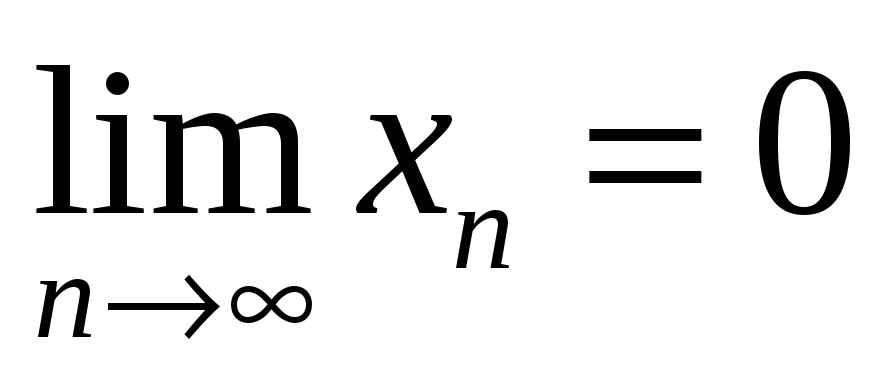, то последовательность <xn> называется бесконечно малой.
Если 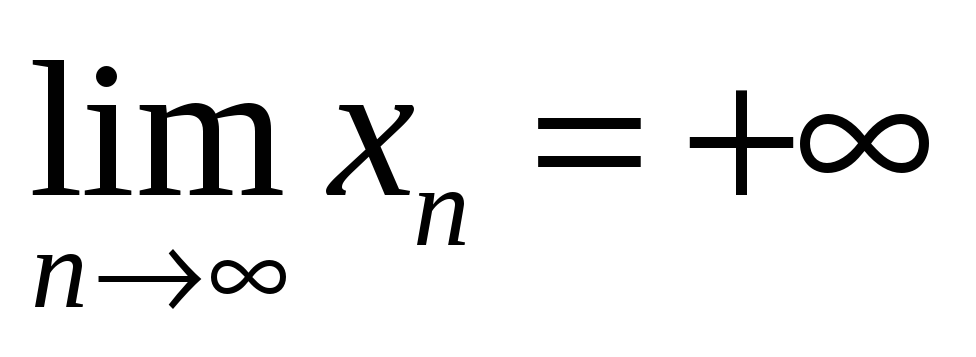– бесконечно большой.
Связь неограниченная бесконечно большая: бесконечно большая неограниченная
бесконечно большая неограниченная. Обратное не верно:
не бесконечно большая
Функцией y = f(x) называется закон, по которому каждому значению xD(f)R ставится в соответствие единственное действительное число yR.
При этом множество значений аргумента D(f) называется областью определения функции, а множество значений <y | y = f(x), xD(f)> называется множеством значений функции.
Функция может быть задана аналитически (то есть формулой), таблично или графически.
Если функция задана таблично, то чтобы найти значение функции для промежуточных значений аргумента применяют интерполяцию, заменяя функцию линейной, квадратичной на участке между двумя значениями аргумента.
Пусть точка x0 является предельной точкой области определения функции, тогда
для > 0 > 0: xD(f) O(x0) \ <x0>: f(x) O(A)
для > 0 > 0: x:
для > 0 > 0: x:
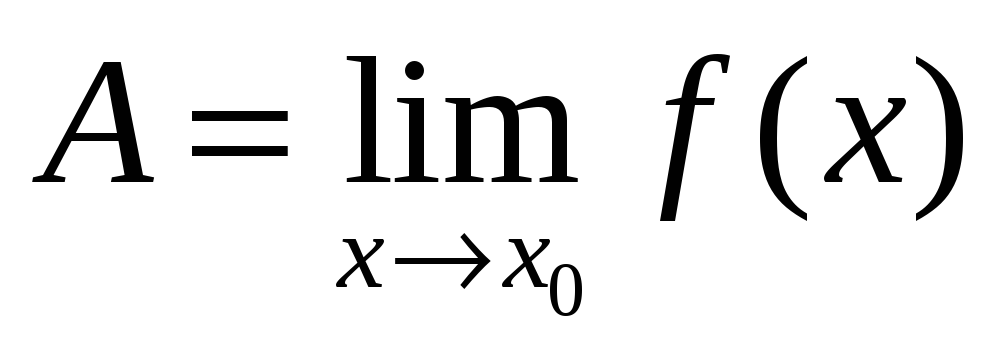
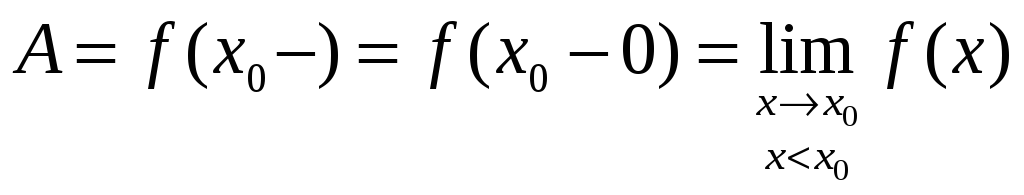
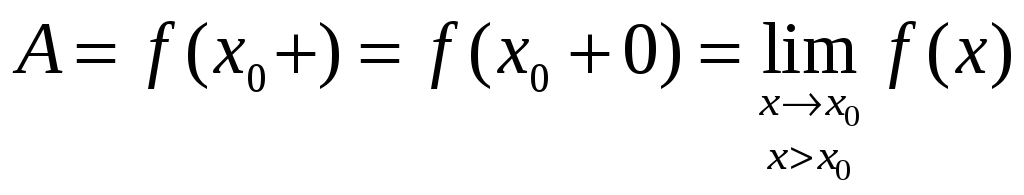
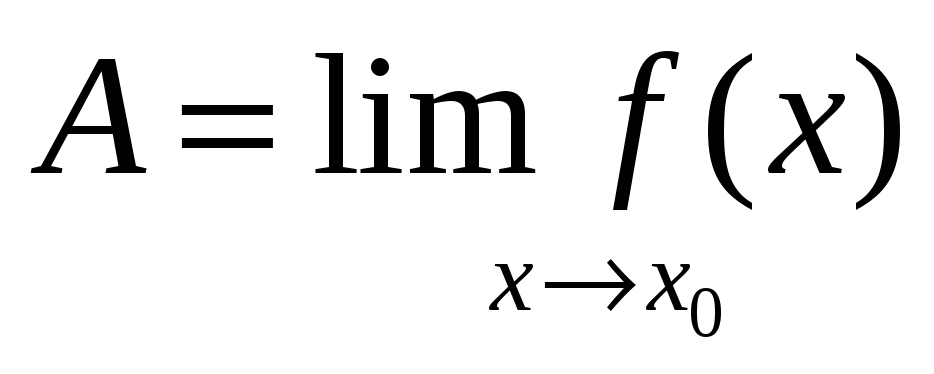
Функция f(x) называется непрерывной в точке x0, если:
.
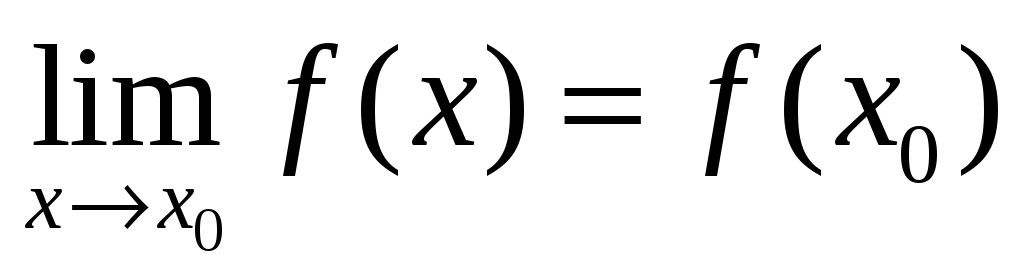
На языке пределов: функция f(x) называется непрерывной в точке x0, если она:
1) определена в этой точке;
2)
На языке ε и δ: функция f(x) называется непрерывной в точке x0, если:
1)
1. Если x0 является предельной точкой D(f)
f(x0+) = A 2 / |x|)
Если функция непрерывна в каждой точке множества X, то она непрерывна на множестве X.
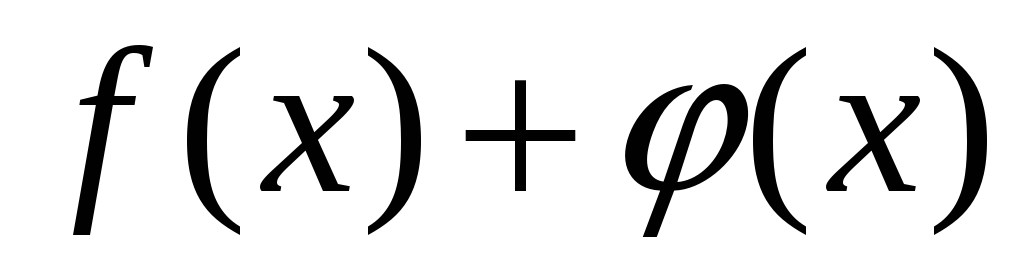
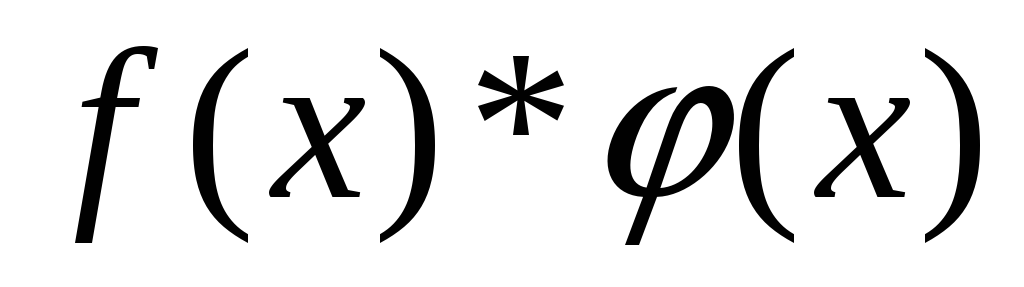
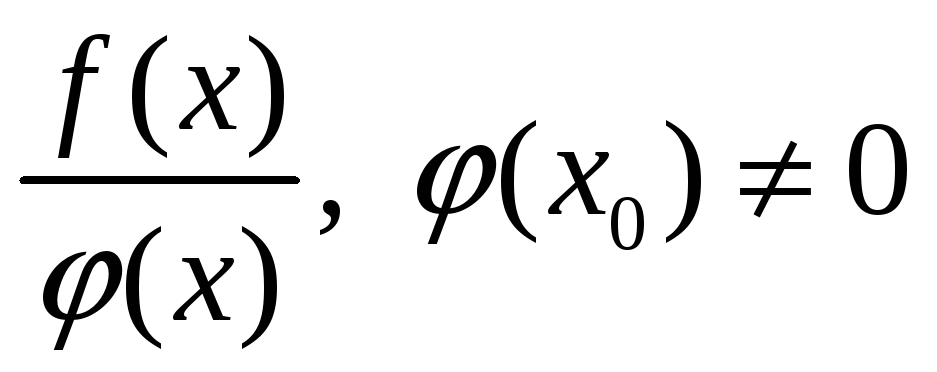
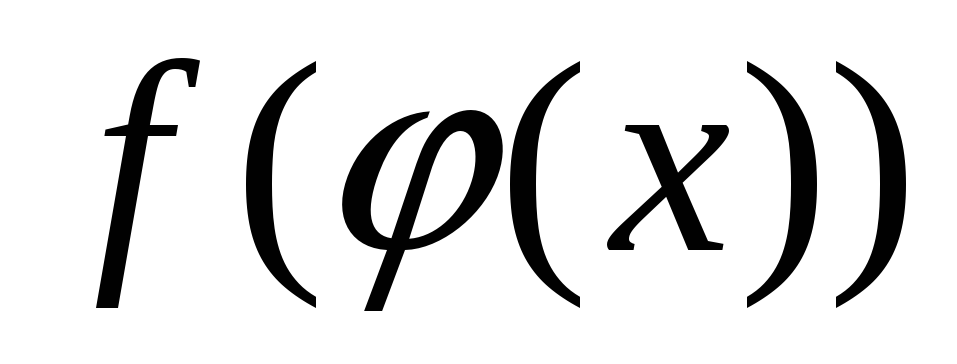
Сумма , произведение , частное, суперпозиция есть функция непрерывная.
Все элементарные функции непрерывны в своей области определения
Элементарные функции из основных элементарных получаются с помощью конечного числа операций сложения, деления, умножения, суперпозиции.
Исследовать на непрерывность, точки разрыва
Функция элементарна. В своей области определения непрерывна
0 – предельная точка для ОДЗ. Но функция не определена в 0 это точка разрыва.
– разрыв II рода.
– неэлементарная функция
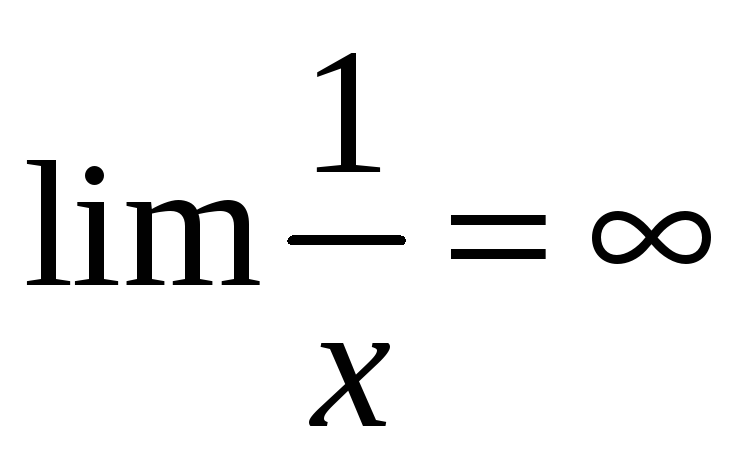
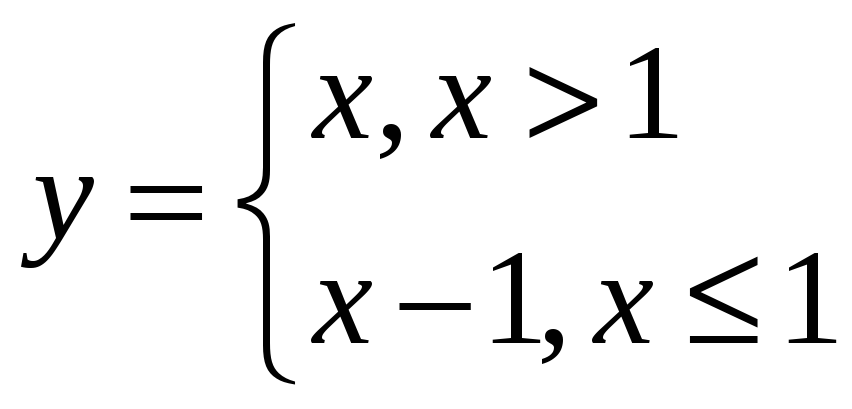
Определение непрерывности функции по Гейне
Функция непрерывна в точке x0, если:
1. она определена в точке x0, то есть ;
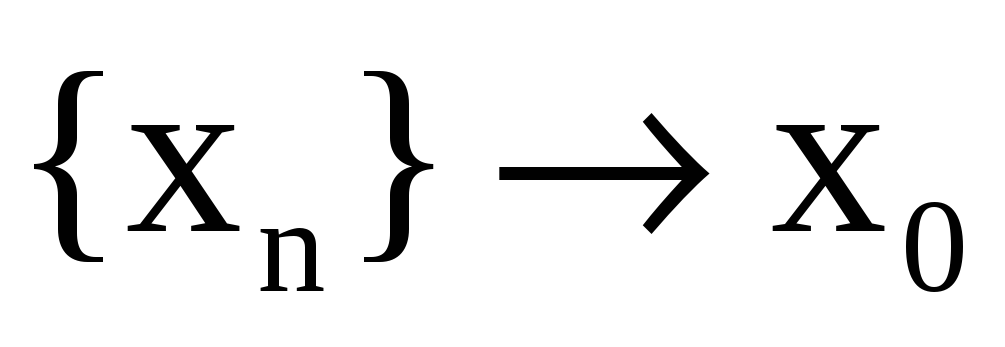
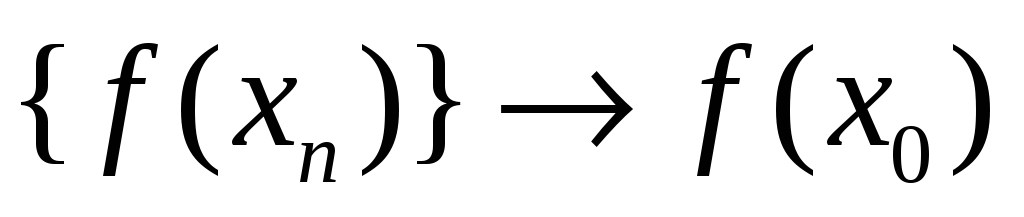
2. для последовательность .
Функция Дирихле определена, но разрывна во всех точках